Studio di funzione

Cos'è lo studio di funzione

Avete già incontrato lo studio di funzione qualche anno fa. Vi era stato detto che era formato da 5 steps, vi hanno mostrato i primi 3 e vi hanno detto che più avanti avrete studiato gli ultimi 2. Oggi è il giorno in cui li studierete.

Quello che noi vogliamo fare è disegnare un grafico quantitativo della nostra funzione. Per grafico quantitativo si intende un grafico che non è esatto al 100\%, ma che rende correttamente l'andamento della funzione.

Come anticipato poco fa, lo studio di funzione è formato dai seguenti 5 steps:

1. Trovare il dominio della funzione.
2. Studiare il segno della funzione.
3. Calcolo dei limiti e degli asintoti.
4. Studio del segno della derivata.
5. Studio del segno della derivata seconda.

Talvolta, all'interno dello step numero 2 viene aggiunto anche lo studio di eventuali simmetrie e periodicità.

Alla fine di ogni passaggio, si ridisegna il grafico precedente modificandolo rispettando le nuove informazioni ottenute.

Nel corso della lezione, porteremo avanti, step per step, lo studio della funzione f(x) = {x^3 -2x + 1\over x+1}

Analizziamo uno per uno ogni step:

Dominio della funzione

Il dominio di una funzione f(x) è l'insieme formato da tutti i numeri reali x tali che f(x) sia ben definita.

Dobbiamo eliminare dal dominio tutti i valori di x che:

Annullano un denominatore. Non possiamo avere un denominatore pari a 0 perché non si può dividere per 0.

Rendono negativo un radicando di una radice con indice pari. Cioè, dentro radici quadrate, quarte, seste, ecc. ... non dobbiamo trovarci numeri negativi, perché nei numeri reali non esistono radici con indice pari di numeri negativi.

Rendono negativo o uguale a 0 l'argomento di un logaritmo. Questo perché non esistono nei numeri reali logaritmi di numeri negativi e non esiste nemmeno il logaritmo di 0.

Creano problemi con altre funzioni presenti. Per esempio, se nella nostra funzione abbiamo \tan(x), dobbiamo escludere dal dominio x={\pi \over 2} + k\pi, dove k è un numero intero, perché la tangente non è ben definita in quei punti.

Effettuando questi 4 passaggi sarete capaci di trovare il dominio di tutte le funzioni che incontrerete.

Nel nostro esempio, quindi, l'unico problema che possiamo incontrare è che il denominatore sia uguale a 0. Vediamo quando questo succede:

x+1=0

x=-1

Dobbiamo quindi escludere soltando -1 dal dominio. Quindi esso sarà:

D_x = (-\infty; -1) \cup (1; +\infty)

Segno della funzione

Risulta importante conoscere il segno della funzione. Dunque, andremo a risolvere la disequazione:

f(x) \geq 0

I punti in cui è verificata l'uguaglianza f(x)=0, vengono chiamati gli zeri della funzione e rappresentano le intersezioni della funzione con l'asse x.

Una volta risolta la disequazione f(x)\geq 0 che ci dice quando la funzione è positiva o uguale a 0, non c'è alcun bisogno di risolvere la disequazione f(x) < 0.

Infatti, se una funzione non è maggiore o uguale a 0, vuol dire che deve essere negativa. Quindi ci basterà prendere i punti esclusi dalla disequazione f(x)\geq 0 che abbiamo già risolto.

Ricordatevi, però, di prendere solo i punti appartententi al dominio.

A volte, arrivati a questo punto, si studiano eventuali simmetrie della funzione e periodicità.

Una funzione è detta pari se per ogni x è vero che f(-x)=f(x). In altre parole, una funzione è pari se è simmetrica rispetto all'asse y:

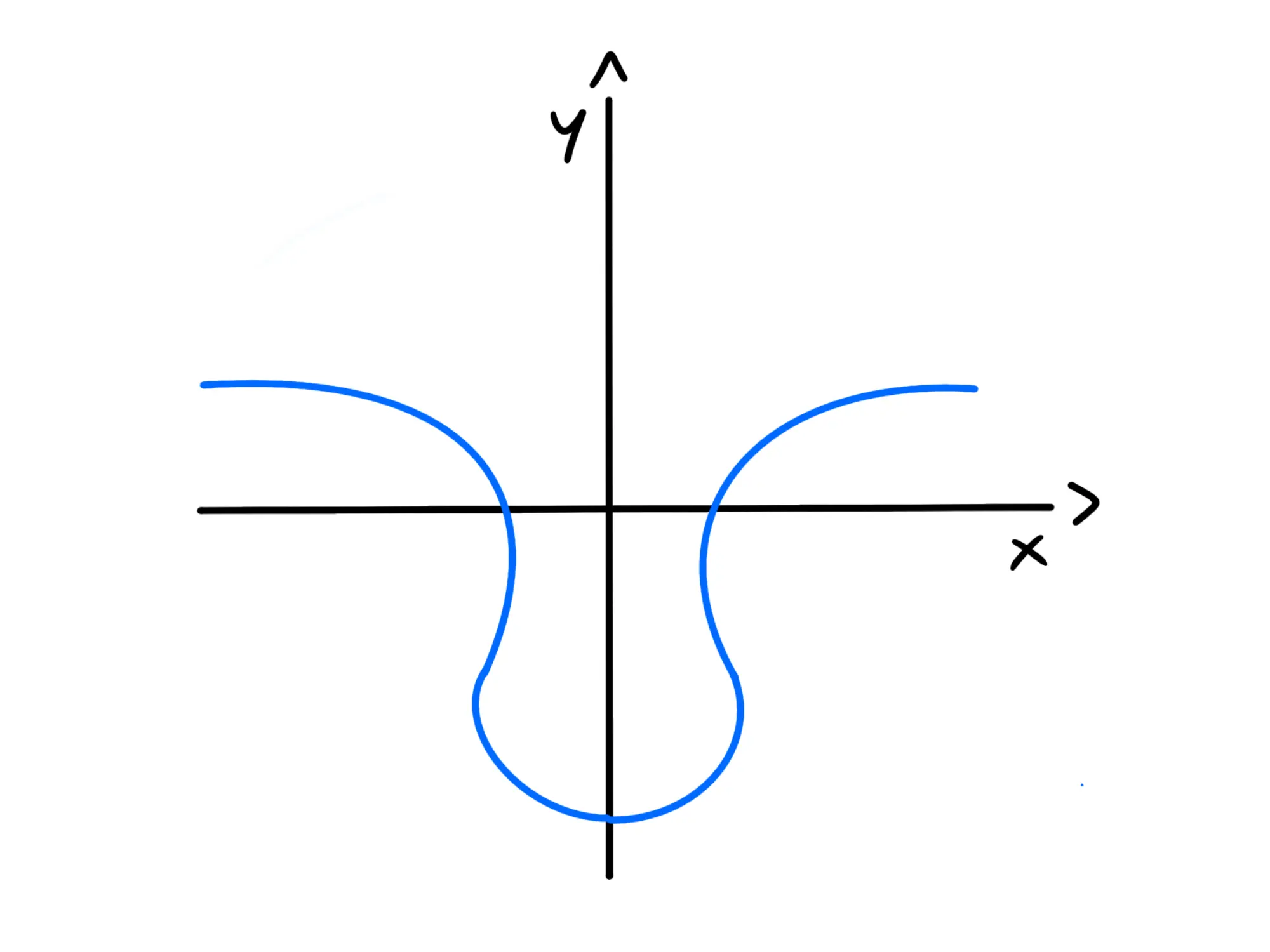
Una funzione è detta dispari se per ogni x è verificato che f(-x) = -f(x). In altre parole, se la funzione è simmetrica rispetto alla retta y=x:

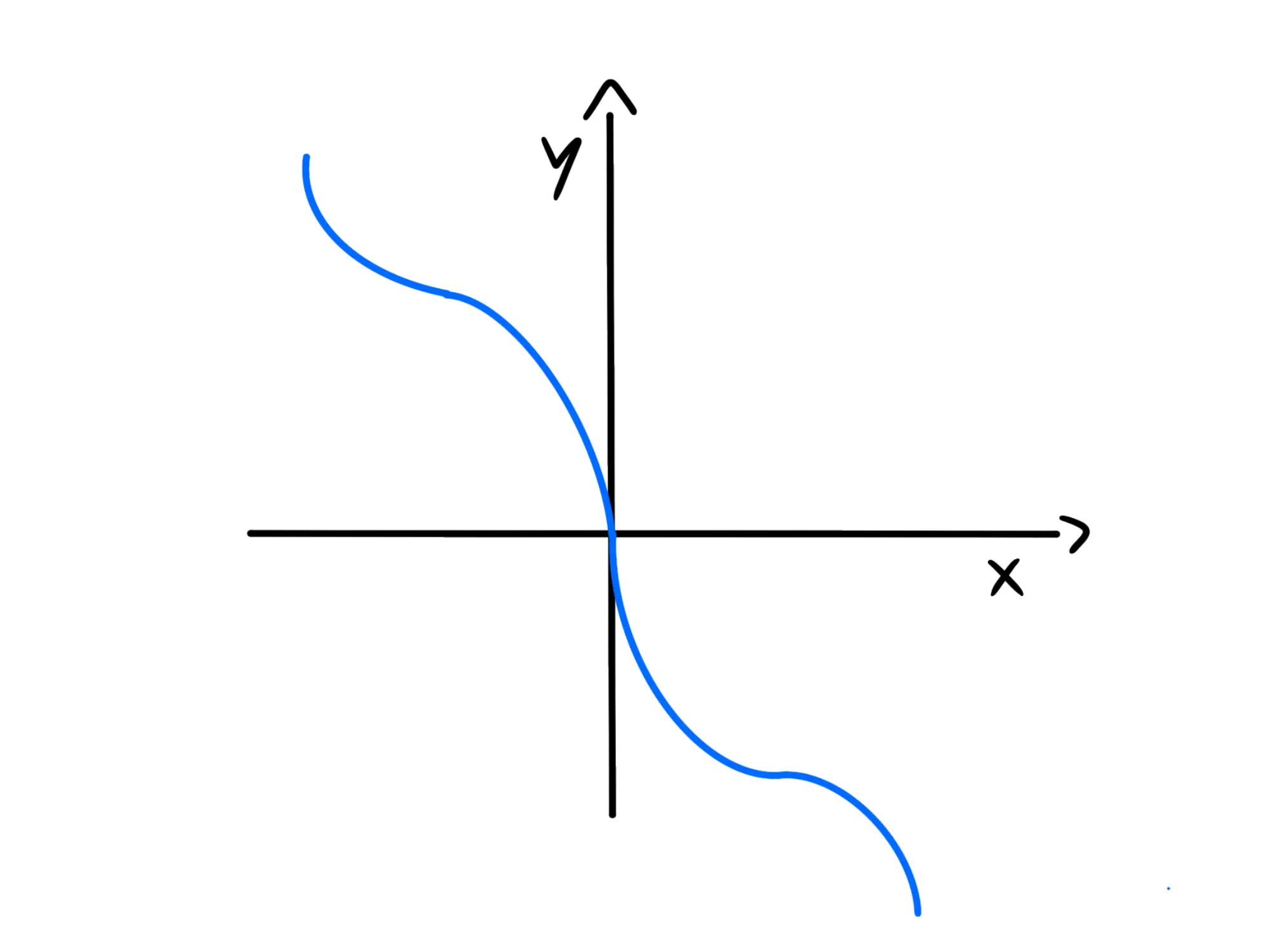
Fate attenzione, al contrario del concetto di numero pari e numero dispari, una funzione che non è pari non deve essere dispari. Infatti, la maggior parte delle funzioni, in realtà, non è nè pari nè dispari.

Alcune funzioni, poi, soprattutto se formate da funzioni trigonometriche, possono essere periodiche.

Nel nostro esempio, quindi, avremo:

{x^3 - 2x + 1\over x+1} \geq 0

Il segno del denominatore è abbastanza semplice da studiare, ma ci conviene fattorizzare il numeratore.

Notiamo che 1 azzera il numeratore, dunque possiamo applicare ruffini ed ottenere:

x^3 - 2x + 1= (x-1) (x^2 + x -1)

Le soluzioni del fattore di secondo grado sono -1+\sqrt{5} \over 2 e -1-\sqrt{5} \over 2 e il coefficiente del termine di secondo grado è positivo, di conseguenza la parabola associata sarà negativa tra le intersezione e positiva altrove.

Da questa fattorizzazione otteniamo quindi già che gli zeri della funzione sono 1, {-1+\sqrt{5}\over 2} e {-1-\sqrt{5}\over 2}.

Per risolvere la disequazione, invece, possiamo tracciare il grafico dei segni:

Dunque avremo f(x)>0 per x< {-1-\sqrt{5}\over 2} \vee -1 < x < {-1+\sqrt{5}\over 2} \vee 1 < x.

Notiamo, poi, che l'intersezione con l'asse y avviene a:

f(0)={0+0+1\over 0+1}= 1

Possiamo quindi indicare in quali aree si troverà la funzione:

Passiamo ora al prossimo step:

Limiti ed asintoti

Per poter tracciare meglio il grafico qualitativo della funzione, è fondamentale studiare alcuni limiti della funzione e osservare se sono presenti asintoti.

Quali limiti dobbiamo risolvere? Bisogna studiare il limite della funzione quando tende ai punti di inizio e di fine di ogni intervallo del dominio.

Se, ad esempio, il dominio della nostra funzione è il seguente:

D_x = (-\infty ; 0) \cup (0;+\infty)

Studieremo il limite della funzione per x che tende a -\infty, a 0^-, a 0^+ e a +\infty.

Risolvendo questi limiti, scopriremo se la funzione presenta degli asintoti. Gli asintoti possono essere orizzontali (solitamente presenti quando x tende \pm \infty), verticali (soprattutto presenti quando x tende ad un punto in cui non è definita la funzione) e obliqui (solitamente presenti quando i limiti per x che tende ai due infiniti sono due infiniti di segno opposto):

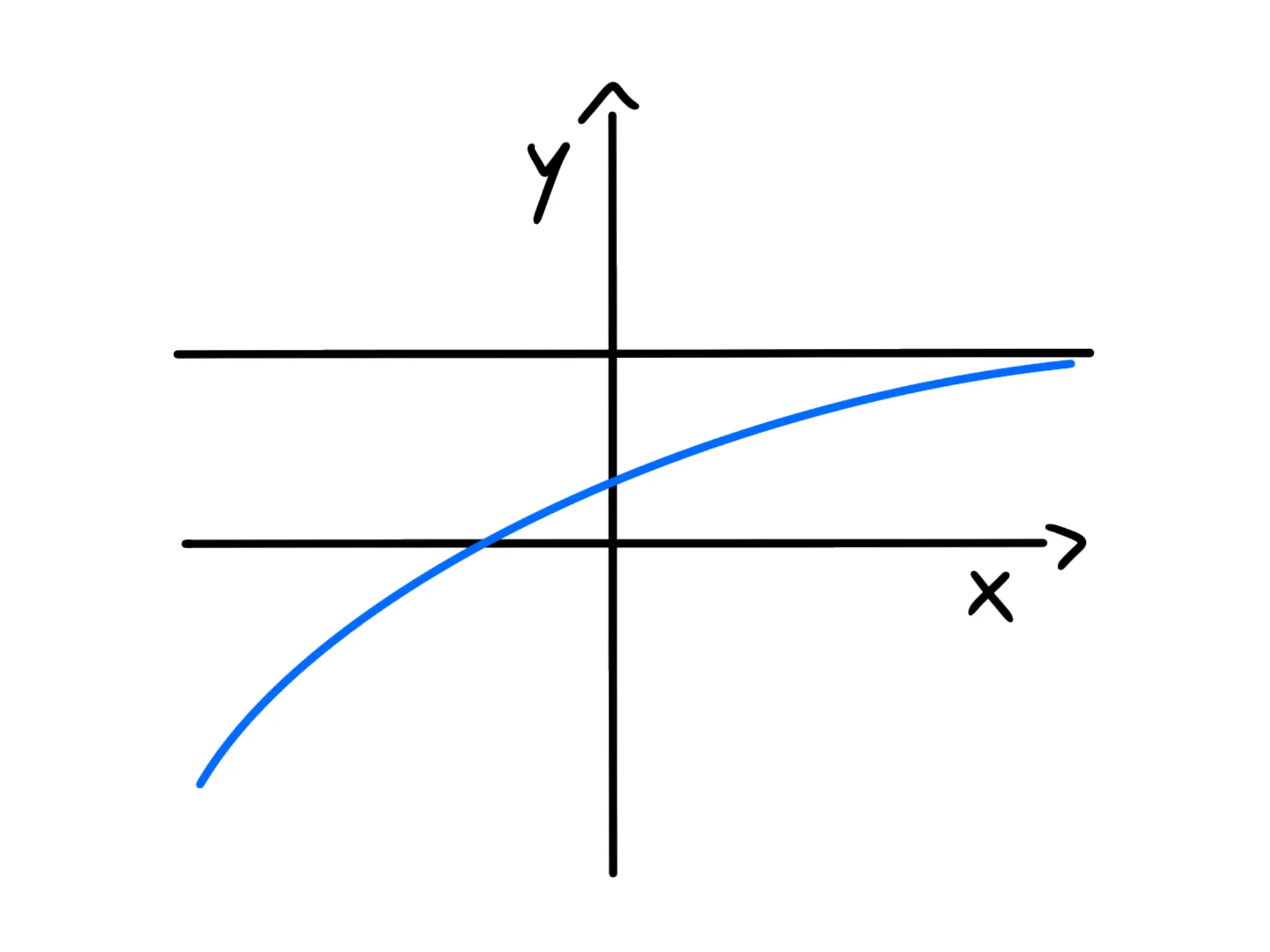
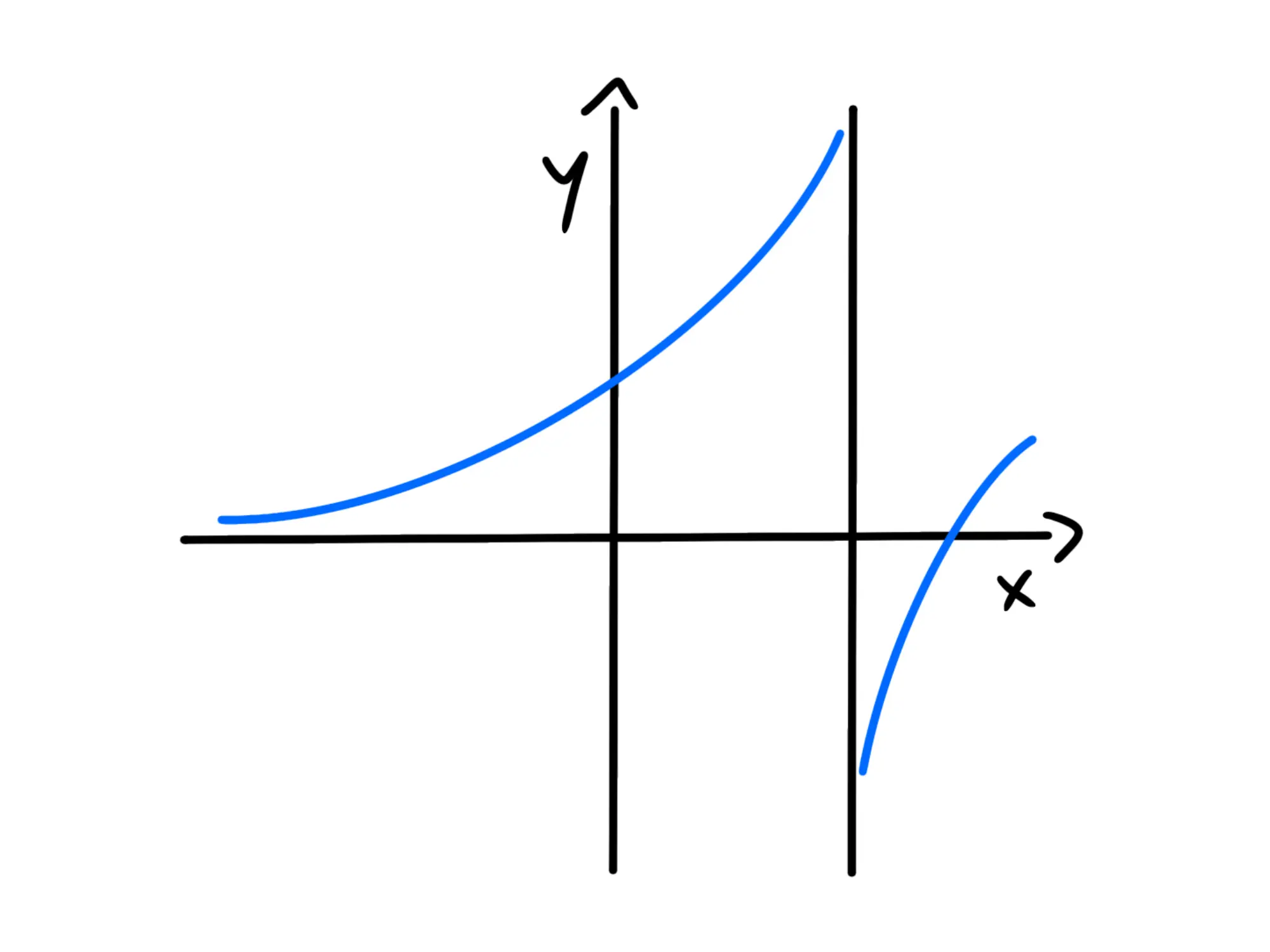
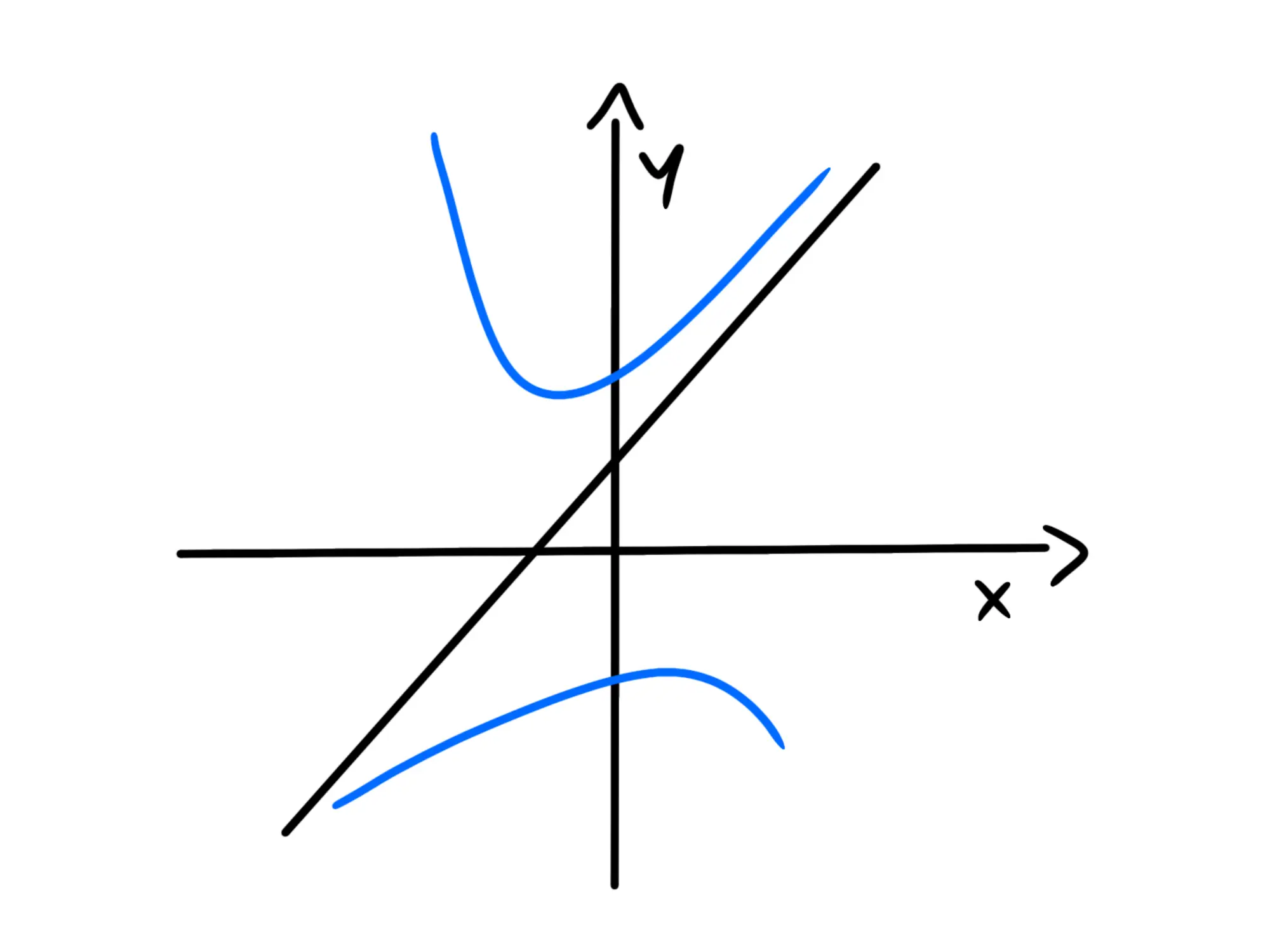
Non tutte le funzioni presentano asintoti, ma non sono rari da incontrare.

Continuiamo con il nostro esempio: prenderemo i limiti per x che tende ad +\infty, a -\infty, a -1^- e a -1^+.

Risolviamoli:

\displaystyle \lim_{x\to +\infty} {x^3 - 2x +1 \over x+1} =\displaystyle \lim_{x\to +\infty} x^2 = +\infty

\displaystyle \lim_{x\to -\infty} {x^3 - 2x +1 \over x+1}= \displaystyle \lim_{x\to -\infty} x^2 = +\infty

\displaystyle \lim_{x\to -1^- } {x^3 - 2x +1 \over x+1} = \displaystyle \lim_{x\to -1^-} {2\over x+1} = -\infty

\displaystyle \lim_{x\to -1^+} {x^3 -2x+1 \over x+1} = \displaystyle \lim_{x\to -1^+} = {2 \over x+1} = +\infty

Dunque avremo che x=-1 sarò un asintoto verticale, mentre non avremo asintoti orizzontali nè obliqui.

Possiamo quindi disegnare l'andamento approssimativo della funzione:

Già avendo effettuati questi 3 steps, infatti, dovreste essere capaci di disegnare un grafico qualitativo molto approssimativo della funzione. Spesso, però, risulta utile studiare se sono presenti massimi o minimi locali:

Studio del segno della derivata

Ci ricordiamo che abbiamo da poco imparato ad usare un nuovo strumento: la derivata. Essa ci dice se la funzione sta aumentando o diminuendo.

Se la derivata è positiva, la funzione sta aumentando, mentre se è negativa sta diminuendo. Dunque sarebbe molto utile studiare il segno della derivata.

Avendo trovato il segno della derivata, potremo tracciare meglio il grafico qualitativo perché sapremo quando sta aumentando e quando sta diminuendo, ma come facciamo a trovare i massimi e i minimi?

Intanto dobbiamo osservare le differenze tra massimi e minimi locali (o relativi) e massimi e minimi assoluti (o globali).

Il massimo assoluto della funzione è il valore più grande che può assumere. Analogamente, il minimo assoluto è il valore minimo che la funzione può assumere.

Un punto, invece, è un massimo locale se è maggiore sia dei valori immediatamente precedenti che quelli immediatamente successivi. Si tratta invece di un minimo locale se è minore dei valori immeditamente precedenti e immediatamente successivi:

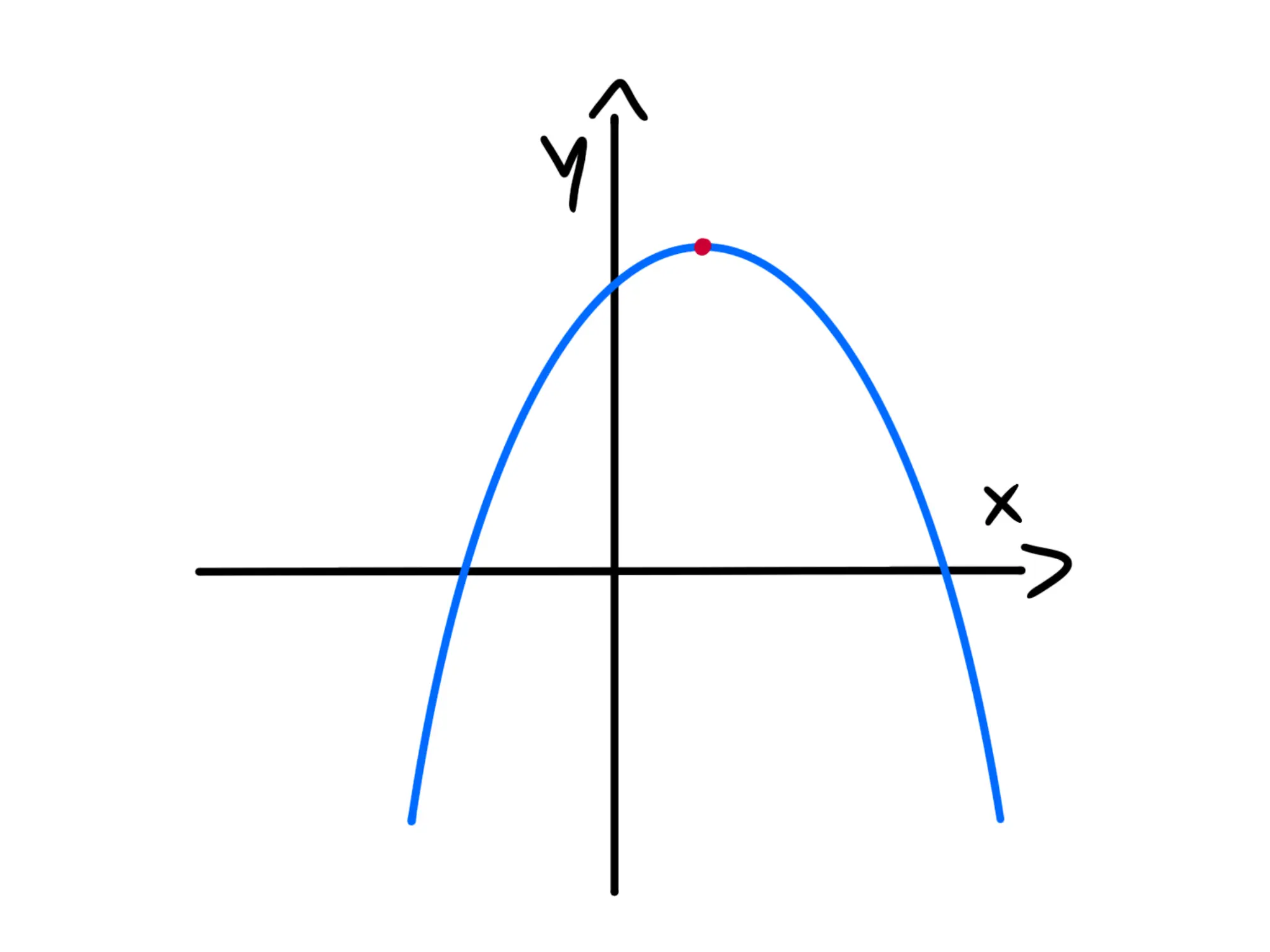
Quali sono più interessanti? Quelli locali o quelli assoluti? Entrambi sono importanti, ma siccome ci possono essere più massimi locali e solo un massimo assoluto, spesso si spende più tempo a studiare i massimi locali.

Come trovare, però, un massimo o un minimo locale?

Affinchè un punto sia un massimo locale, dobbiamo avere che prima di esso la funzione stia aumentando e subito dopo di esso cominci a diminuire. In altre parole, la derivata della funzione prima di esso deve essere positiva e dopo di esso deve essere negativa.

Quando è che una funzione da positiva diventa negativa? Quando passa per 0. I massimi e i minimi locali avvengono quando la derivata è uguale a 0 e cambia segno.

Se da positiva diventa negativa, otteniamo un massimo. Se da negativa diventa positiva, otteniamo un minimo. E se la derivata è positiva, diventa 0 e rimane positiva? In tal caso, otteniamo un punto flesso.

Un punto flesso è detto a tangente orizzontale ascendente se la derivata è positiva, mentre è detto a tangente orizzontale discendente se la derivata è negativa:

Non ci basta quindi sapere quando la derivata è uguale a 0, dobbiamo anche sapere che segno ha prima e dopo, per questo è molto importante studiare il segno della derivata.

Inoltre, potremmo avere un punto in cui la funzione è ben definita, ma la sua derivata no. In tal caso, abbiamo 3 possibilità:

Se la derivata non esiste perchè il limite destro è diverso dal limite sinistro, ma entrambi danno numeri finiti, otteniamo un punto angoloso:

Se il limite destro e sinistro della derivata sono uguali, ma danno +\infty o -\infty, otteniamo un punto flesso a tangente verticale:

Infine, se il limite destro è uguale a +\infty e quello sinistro è pari a -\infty o viceversa, otteniamo una cuspide:

Procediamo con il nostro esempio: per prima cosa troviamo la derivata prima della nostra funzione:

f'(x) = {d\over dx} {x^3 - 2x +1 \over x+1}=

= {({d\over dx}(x^3 - 2x +1)) \cdot (x+1) - (x^3 - 2x + 1) \cdot {d\over dx}(x+1) \over (x+1)^2}=

={2x^3 + 3x^2 -3 \over (x+1)^2}

Il denominatore è sempre maggiore di 0, mentre studiando più approfonditamente il numeratore si può ottenere che esso sarà maggiore di 0 per x maggiore di circa 0.80644.

Dunque, prima è negativa e poi diventa positiva, questo vuol dire che abbiamo un minimo locale per x=0.80644 circa. Oltre ad essere un minimo locale è pure il minimo assoluto? No, perché sappiamo che la nostra funzione tende a -\infty quando x tende a -1^-.

Siccome la derivata ha solo uno zero, non ci saranno altri punti di massimo o minimo locali.

Sapendo, inoltre, che la nostra funzione è monotona decrescente per x< 0.80644 circa per poi diventare monotona crescente, possiamo ridisegnare meglio il grafico:

Abbiamo quasi finito il nostro studio di funzione, ci rimane soltanto da studiare la concavità della nostra funzione:

Studio della derivata seconda

Oltre al segno della derivata prima, risulta utile studiare anche il segno della derivata seconda, cioè la derivata della derivata. Infatti, esso ci dice che concavità possiede la nostra funzione:

Se in un intervallo la derivata seconda è positiva, la nostra funzione ha concavità verso l'alto (cioè la funzione è convessa) in quell'intervallo.

Se, invece, in un intervallo la derivata seconda è negativa, la funzione ha concavità verso il basso (cioè la funzione è concava) in quell'intervallo.

I punti in cui la concavità cambia da verso l'alto al verso il basso sono i punti di flesso.

Concludiamo quindi il nostro esempio di studio di funzione. Calcoliamo la sua seconda derivata:

f''(x) = {d\over dx} {2x^3 + 3x^2 + 3\over (x+1)^2}=

={2(x^3 + 3x^2 + 3x + 3)\over (x+1)^3}

Possiamo riscrivere x^3 + 3x^2 + 3x + 3 come x^3 + 3x^2 + 3x + 1 +2, che quindi diventa (x+1)^3 +2.

Sostituiamo e risolviamo la disequaizone:

{2(x+1)^3 + 4 \over (x+1)^3} \geq 0

Studiamo prima il segno del denominatore:

2(x+1)^3 +4 \geq 0

(x+1)^3 \geq -2

La radice cubica è un operatore che preserva il segno, dunque possiamo applicarlo su entrambi i lati dell'equazione:

x+1 \geq \sqrt[3]{-2}

x \geq -1 -\sqrt[3]{2}

Per il denominatore, invece, abbiamo:

(x+1)^3 \geq 0

x \geq -1

Possiamo quindi tracciare il grafico dei segni:

La nostra funzione avrà quindi concavità verso l'alto per x< -1 -\sqrt[3]{2} \vee x>-1 e quindi concavità verso il basso per -1-\sqrt[3]{2} < x < -1. L'unico 0 che abbiamo è a x= -1-\sqrt[3]{2}, quindi quello sarà l'unico punto di flesso.

Con queste informazioni, possiamo tracciare il grafico definitivo:

In generale, una volta raccolte tutte queste informazioni, sarete capaci di tracciare un buon grafico quantitativo della funzione.

1.

Studia e poi traccia il grafico probabile della seguente funzione: y = \sqrt[3]{x^2(x-1)}.

Soluzione Passaggi

Dobbiamo iniziare cercando il dominio: siccome abbiamo una radice cubica, cioè una radice di indice dispari, non ci sono problemi di esistenza. Non essendoci poi altre problematiche, il dominio coinciderà con l'insieme dei numeri reali.

Passiamo quindi al segno e alle intersezioni con gli assi:

Per il segno imponiamo la funzione maggiore di 0 e vediamo per quale x è verificata:

\sqrt[3]{x^2 (x-1)} \geq 0

Siccome la radice cubica permane il segno, possiamo toglierla e guardare soltanto al radicando:

x^2 (x-1) \geq 0

x^2 è sempre positivo, dunque possiamo toglierlo (sapendo però che così escludiamo il caso x=0 per cui infatti otteniamo 0) e guardare solo a x-1:

x-1 \geq 0

x \geq 1

Per l'intersezione con l'asse y basta imporre x=0, ottenendo y = \sqrt[3]{0^2(0-1)} = 0.

Dunque il grafico passa per l'origine.

Per trovare le intersezioni con l'asse x bisogna invece imporre y=0, ottenendo \sqrt[3]{x^2(x-1)} = 0, da cui otteniamo:

x^2 (x-1) = 0

x= 0 \vee x = 1

Dunque le intersezioni sono a x= 0 (infatti il grafico passava per l'origine) e ad x=1.

Ora, per tracciare il grafico probabile, ci resta solo da studiare gli asontitoti:

Non essendoci valori finiti esclusi dal dominio, non possono esserci asintoti verticali. Calcoliamo dunque il limite per x che tende a +\infty e -\infty per cercare gli asintoti orizzontali:

\displaystyle \lim_{x \to +\infty} \sqrt[3]{x^2 (x-1)} = \sqrt[3]{+\infty} = + \infty

\displaystyle \lim_{x \to -\infty} \sqrt[3]{x^2 (x-1)} = \sqrt[3]{+\infty \cdot -\infty} = \sqrt[3] {-\infty} = -\infty

Siccome non otteniamo valori finiti ma +\infty e -\infty, non abbiamo asintoti orizzontali. Vediamo dunque se ci sono asintoti obliqui.

Per trovare il coefficiente angolare m della retta, dobbiamo calcolare il limite per x che tende a +\infty e a -\infty della funzione fratto x:

m = \displaystyle \lim_{x \to +\infty} {\sqrt[3]{x^2 (x-1)}\over x} = \displaystyle \lim_{x\to +\infty} {\sqrt[3]{x^3 - x^2 \over x^3}} = \displaystyle \lim_{x \to +\infty} \sqrt[3]{1 - {1\over x}} = \sqrt[3]{1 - {1\over +\infty}} = 1

Facendo il limite per x che tende a -\infty otteniamo lo stesso valore.

Per trovare l'ordinata all'origine q dobbiamo fare il limite per x che tende a +\infty e a -\infty della funzione meno mx (siccome abbiamo ottenuto m=1, dovremo fare -x):

q = \displaystyle \lim_{x\to +\infty} (\sqrt[3]{x^2 (x-1)} - x) = \displaystyle \lim_{x\to +\infty} ({x^3 - x^2 - x^3\over (\sqrt[3]{x^3 - x^2})^2 + x\sqrt[3]{x^3 - x^2} + x^2 }) = \displaystyle \lim_{x \to +\infty} {-x^2 \over x^2 + x^2 + x^2} = -{1\over 3}

Nel calcolo di questo limite siamo andati un po' veloci per non appensantire con i troppi calcoli. Abbiamo razionalizzato sfruttando il prodotto notevole della differenza di due cubi, poi abbiamo portato fuori dalle radici i termini di grado più alto e cancellato tutti i termini del tipo {1\over x} o con altre potenze di x al denominatore perché quando dividiamo per +\infty otteniamo 0.

Infine, ottenendo due polinomi dello stesso ordine, abbiamo fatto il rapporto dei coefficienti ottenendo -{1\over 3}.

Otteniamo lo stesso risultato pure quando x tende a -\infty. Quindi dobbiamo avere che la retta y = x - {1\over 3} è asintono obliquo sia per x che tende a +\infty che per x che tende a -\infty.

L'ultima cosa da controllare è se e dove la funzione interseca l'asintoto. Per farlo basta eguagliare le due equazioni:

\sqrt[3]{x^3 - x^2} = x - {1\over 3}

x^3 - x^2 = (x - {1\over 3})^3

x^3 - x^2 = x^3 - x^2 + {1\over 3} x - {1\over 27}

0 = {1\over 3}x - {1\over 27}

x = {1\over 9}.

Con tutte queste informazioni ora possiamo tracciare il grafico probabile della funzione:

---

2.

Studia completamente la seguente funzione e tracciane il grafico: y = {e^x - 1\over e^x +1}.

Soluzione Passaggi

Iniziamo trovando il dominio: l'esponenziale non ha problemi di esistenza, ma abbiamo una frazione, dunque dobbiamo controllare che il denominatore non sia uguale a 0.

Vediamo quindi quando il denominatore si annulla:

e^x + 1 = 0

e^x = -1

Ma l'esponenziale è sempre positivo quindi quest'equazione è impossibile nei numeri reali, perciò, non avendo punti con problematiche, il dominio coinciderà con l'insieme dei numeri reali.

Ora, dunque, dobbiamo studiare il segno. Per farlo imponiamo la funzione maggiore o uguale a 0 e vediamo per quale x è verificata:

{e^x -1 \over e^x + 1 } \geq 0

Siccome e^x è sempre maggiore di 0, anche e^x+1 sarà sempre positivo, quindi è inutile studiare il segno del denominatore. Guardiamo quindi soltanto al numeratore:

e^x -1 \geq 0

e^x \geq 1

x \geq 0

Quindi la funzione sarà positiva per x maggiore di 0 e negativa per x minore di 0.

Adesso vediamo se la funzione è pari o dispari.

Se la funzione è dispari, allora dobbiamo avere f(-x) = -f(x), che notiamo essere verificato:

f(-x) = {e^{-x} -1 \over e^{-x} + 1} = {{1\over e^x} - 1 \over {1\over e^x} +1} = {{1-e^x \over e^x}\over {1+e^x \over e^x}} = {1-e^x\over 1+ e^x } = - {e^x -1 \over e^x +1} = - f(x)

Quindi il grafico sarà simmetrico rispetto all'origine.

Troviamo ora le intersezioni con gli assi cartesiani:

Per trovare le intersezioni con l'asse y basta porre x = 0, ottenendo y = {e^0 - 1\over e^0 + 1 }= 0.

Quindi il grafico passa per l'origine. Per trovare invece le intersezioni con l'asse delle x imponiamo y = 0 ottenendo:

{e^ x -1 \over e^x +1} = 0

e^x - 1 = 0

e^x = 1

x = 0

Infatti il grafico passava per l'origine ed ora sappiamo che quella è l'unica intersezione con gli assi.

Ora passiamo allo studio degli asintoti:

Siccome non ci sono punti finiti esclusi dal dominio, non ci possono essere asintoti verticali.

Calcoliamo i limiti per x che tende a +\infty e a -\infty per vedere se ci sono asintoti orizzontali:

\displaystyle \lim_{x\to +\infty} {e^x -1 \over e^x +1} = 1

\displaystyle \lim_{x\to -\infty} {e^x -1\over e^x +1} = {0-1\over 0+1} = -1

Quindi y=1 è asintoto orizzontale per x che tende a +\infty, mentre y=-1 è asintoto orizzontale per x che tende a -\infty.

Guardiamo se la funzione interseca gli asinoti: poniamo f(x) = 1 e f(x) = -1 e vediamo se ha soluzioni:

{e^x -1 \over e^x +1} = 1

e^x -1 = e^x +1

-1=1

L'equazione è impossibile dunque non ci sono le intersezioni con il primo asintoto, vediamo il secondo:

{e^x -1 \over e^x +1} = -1

e^x -1 = -e^x -1

2e^x = 0

e^x = 0

Anche quest'equazione è impossibile, dunque il grafico non interseca nemmeno il secondo asintoto.

Adesso studiamo la derivata prima per cercare punti di massimo o minimo e per chiarire meglio l'andamento della funzione:

f'(x) = {d\over dx} {e^x -1 \over e^x +1} = {{d\over dx} (e^x -1) \cdot (e^x +1) - (e^x -1)\cdot {d\over dx}(e^x +1) \over (e^x +1)^2} = {e^x (e^x -1) - (e^x-1) e^x \over (e^x +1)^2} = {2e^x \over (e^x+1)^2}

Per trovare la derivata abbiamo usato la regola della derivata di un quoziente. Siccome il numeratore è un esponenziale e il denominatore è un quadrato, la derivata prima di questa funzione è sempre positiva. Questo vuol dire che si tratta di una funzione monotone crescente.

Calcoliamo ora la derivata seconda per trovare la concavità e per vedere se ci sono punti di flesso:

f''(x) = {d\over dx} ({2e^x \over (e^x +1)^2})= {{d\over dx}(2e^x) (e^x +1)^2 - 2e^x \cdot {d\over dx} (e^x +1)^2\over (e^x +1)^4} = {2e^x \cdot(e^x +1)^2 - 2e^x \cdot 2 e^x (e^x +1) \over (e^x +1)^4} = {2e^x (e^x+1) (e^x +1 -2e^x)\over (e^x +1)^4}= {2e^x (e^x +1) (1-e^x) \over (1+e^x)^4}

Notiamo che tutti i fattori tranne 1-e^x sono sempre positivi quindi l'unico che influisce sul segno è proprio quest'ultimo. Siccome 1-e^x > 0 quando x < 0, vuol dire che la derivata seconda è positiva quando x < 0, si annulla quando x = 0 ed è negativa per x > 0.

Da questo otteniamo che la concavità della funzione è verso l'alto quando x < 0, che x = 0 è un punto flesso e per x > 0 la concavità è verso il basso.

Con tutte le informazioni che abbiamo trovato siamo finalmente pronti per tracciare il grafico della funzione:

---