Sfere uniformemente cariche

Cosa devo già sapere?

Da sapere:

Cariche elettriche

Campo elettrico

Flusso del campo elettrico

Campo elettrico per punti esterni alla sfera uniformemente carica

Supponiamo di avere una sfera uniformemente carica, cioè la cui carica è disposta in maniera uniforme lungo tutto il suo volume:

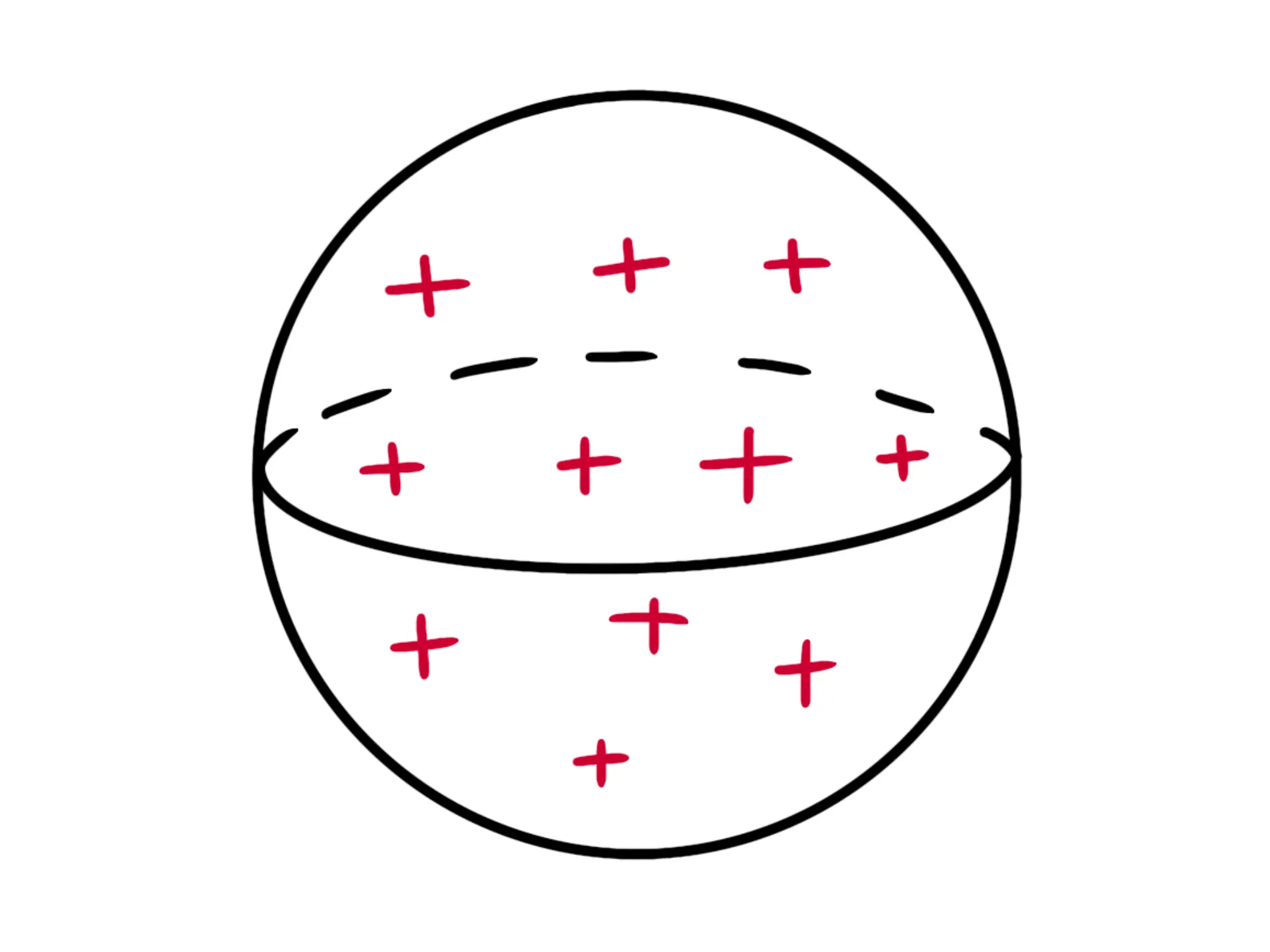
Essa avrà una certa carica Q ed indurrà un certo campo elettrico \overrightarrow{E}.

Se siamo fuori dalla sfera, per questioni di simmetria molto simili a quelle che avevamo visto per il piano e la retta infiniti, la direzione del campo deve essere la retta che congiunge il centro della sfera e P e il verso dipenderà dalla carica (si allontana dalla sfera se Q è positiva, mentre punta verso la sfera se Q è negativa):

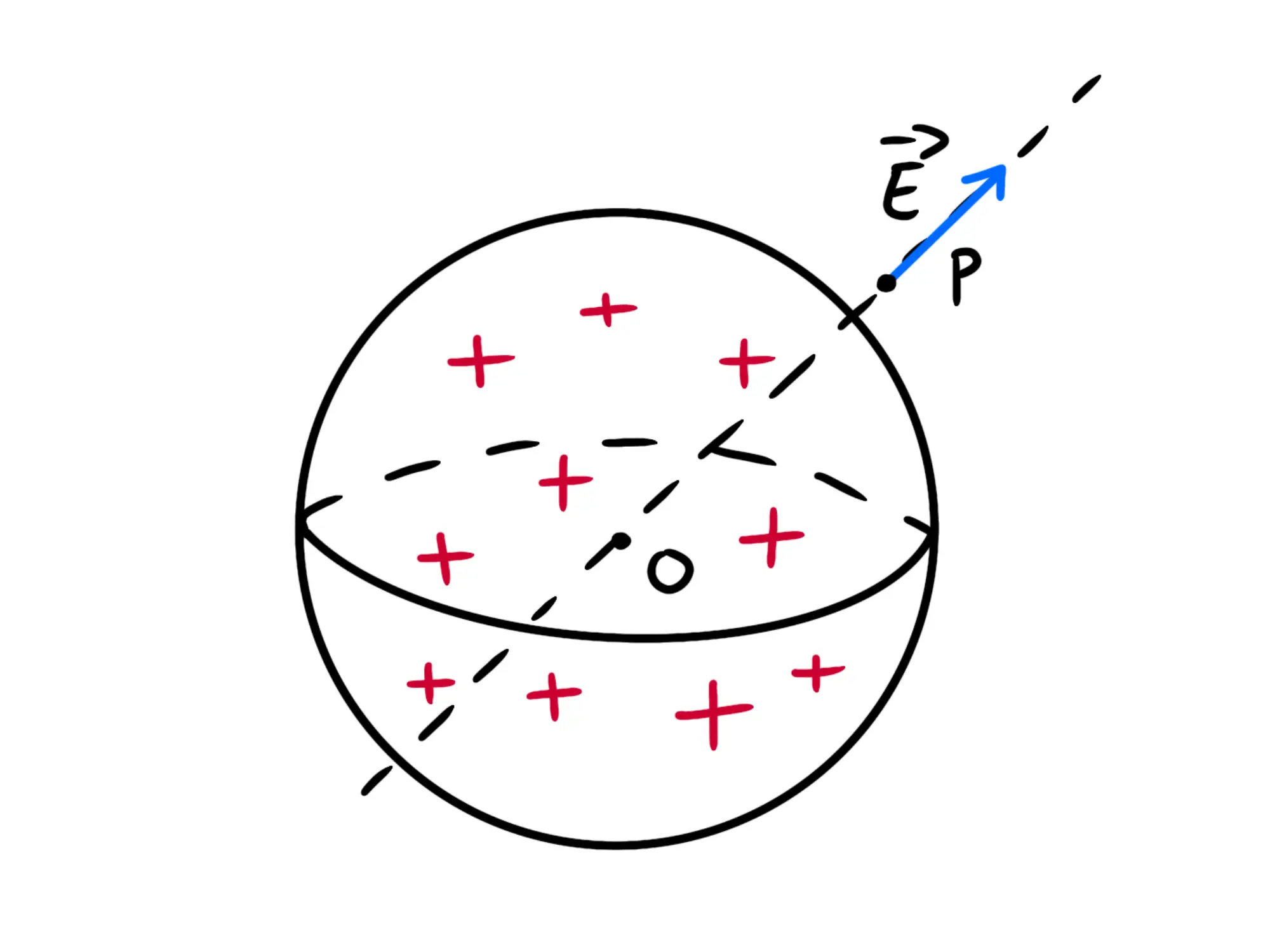
Manca solo da trovare il modulo. Per farlo possiamo usare la solita tecnica che abbiamo già usato per la retta e il piano infiniti: usiamo il teorema di Gauss e la definizione del flusso del campo elettrico per calcolare quest'ultimo in due modi diversi e confrontarli.

Iniziamo usando il teorema di Gauss. Per poterlo applicare ci serve una superficie chiusa \Omega e dobbiamo sceglierla in modo che quando useremo il secondo metodo i conti escano facili.

Per questo, essendo i vettori del campo elettrico disposti a raggiera in tre dimensioni, affinchè i vettori siano sempre perpendicolari alla superficie, conviene prendere una sfera:

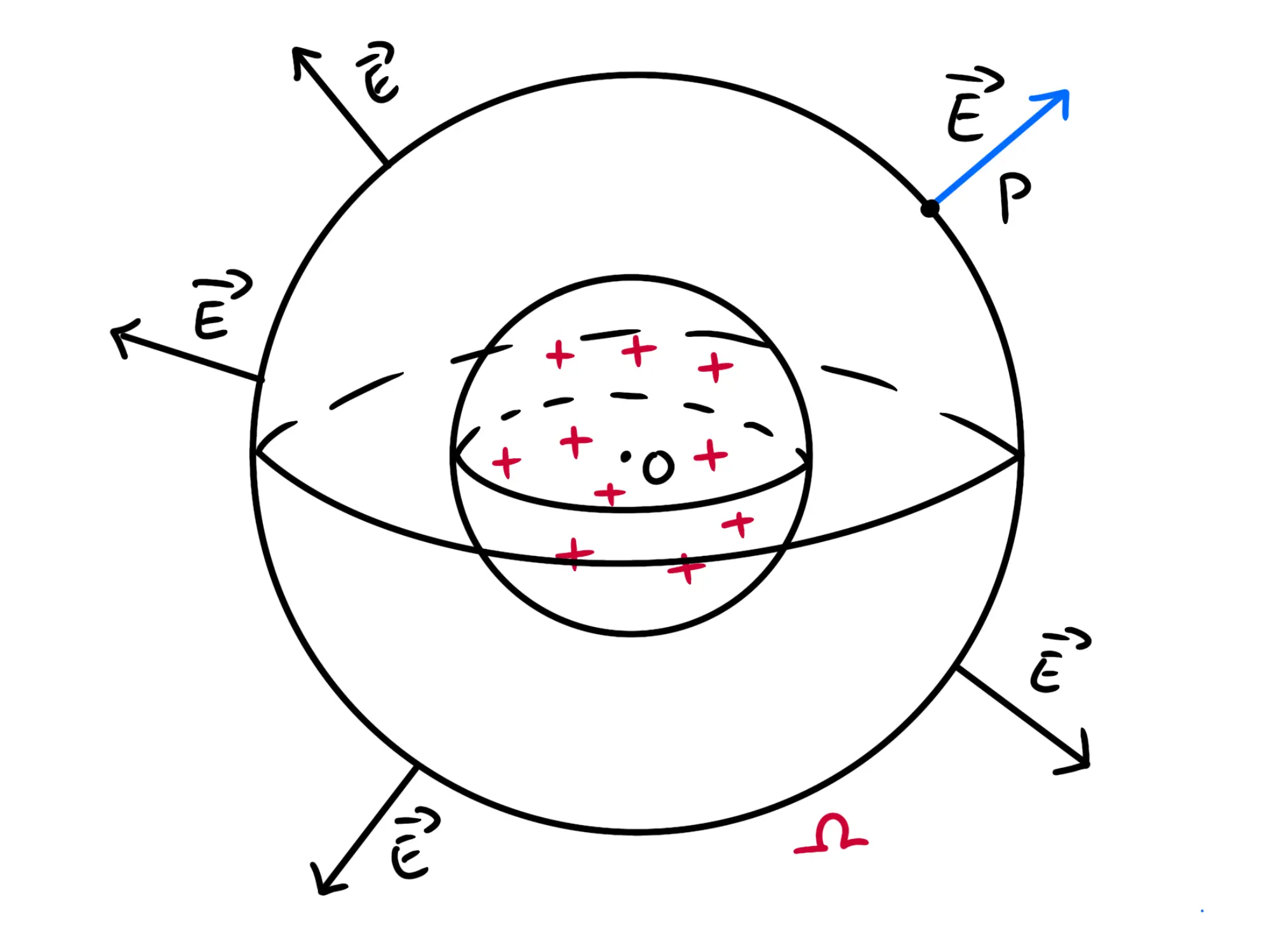
La sfera \Omega contiene tutta la sfera uniformemente carica, dunque contiene tutta la carica Q. Per il teorema di Gauss, dunque, dobbiamo avere:

\Phi_{\Omega}(\overrightarrow{E}) = {Q\over \epsilon_0}

Adesso applichiamo la definizione del flusso del campo elettrico:

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N \overrightarrow{E_i} \cdot \Delta\overrightarrow{ S_i}

Siccome \overrightarrow{E_i} e \Delta\overrightarrow{S_i} sono paralleli, il loro prodotto scalare è uguale al prodotto dei loro moduli, dunque:

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N E_i \cdot \Delta S_i

Siccome ruotando la sfera non cambia niente, è assurdo pensare che i vettori, a parità di distanza, abbiamo modulo diverso. La situazione è totalmente simmetrica, dunque i moduli devono essere uguali. Perciò ogni E_i è uguale ad E, che è dunque una costante nella sommatoria che possiamo dunque portare fuori:

\Phi_{\Omega}(\overrightarrow{E}) = E \sum_{i=1}^N \Delta S_i

Se infine sommo tutte le aree \Delta S_i dei rettangolini in cui ho suddiviso la sfera, otterrò la superficie di tutta la sfera. Se chiamiamo il suo raggio r (che sarà dunque uguale alla distanza del nostro punto P dal centro), siccome l'area della sfera è uguale a 4\pi r^2, dobbiamo avere:

\Phi_{\Omega}(\overrightarrow{E}) = E4\pi r^2

Confrontando questo risultato con quello ottenuto usando il teorema di Gauss otteniamo che:

E4\pi r^2 = {Q\over \epsilon_0}

E = {Q\over 4\pi \epsilon_0 r^2}

Cioè è uguale al campo elettrico indotto da un'unica carica puntiforme posizionata nel centro della sfera.

La formula che abbiamo ottenuto va bene se la carica è positiva. Se invece è negativa, i vettori \overrightarrow{E} e \Delta \overrightarrow{S_i} spaziavano un angolo di 180^{\circ} e dunque il loro prodotto scalare avrebbe avuto un meno davanti. Però questo meno si semplifica con quello della carica negativa Q, dunque possiamo risolvere il problema mettendo il modulo alla carica nella nostra formula:

E = {|Q|\over 4\pi\epsilon_0 r^2}

Ok, ora vediamo cosa succede se invece siamo dentro alla sfera:

Campo elettrico per punti interni alla sfera uniformemente carica

Che succede se invece ci troviamo dentro alla sfera?

In tal caso la situazione cambia. Applichiamo lo stesso procedimento di prima per scoprire quanto vale il campo elettrico:

Prendiamo un punto P e chiamiamo \Omega la sfera che passa per P con lo stesso centro della sfera carica:

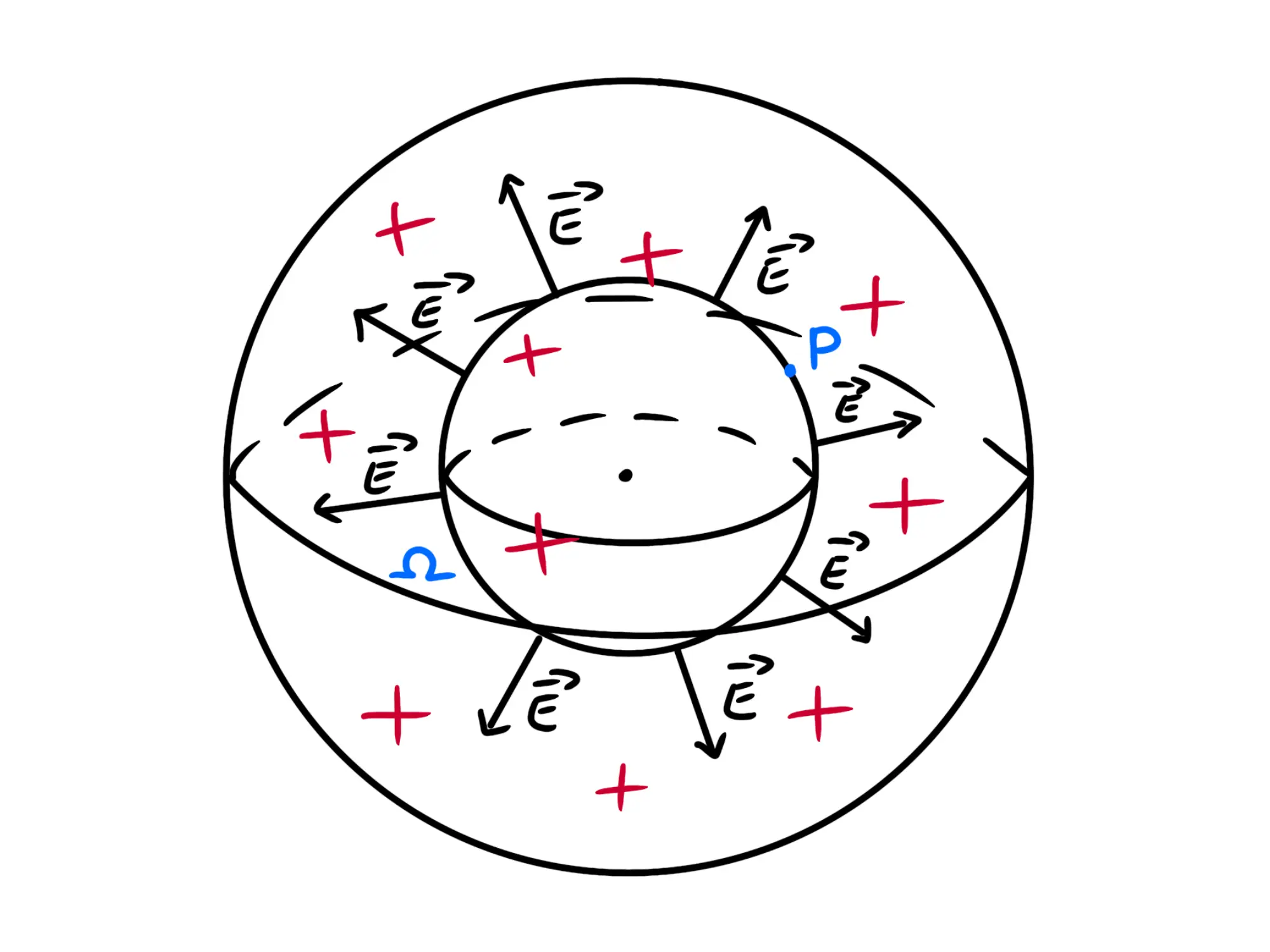
Per le stesse ragioni di simmetria di prima, i vettori di del campo elettrico sulla superificie saranno tutti perpendicolari ad essa ed uguali in modulo.

Per questo avremo, come prima che \overrightarrow{E} \cdot \Delta\overrightarrow{S} = E \Delta S.

Calcoliamo ora, come sempre, il flusso del campo elettrico attraverso \Omega utilizzando la sua definizione e il teorema di Gauss.

Se utilizziamo la formula del flusso \Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N \overrightarrow{E} \cdot \overrightarrow{S}, facendo gli stessi esatti calcoli del capitolo precedente, otteniamo:

\Phi_{\Omega}(\overrightarrow{E}) = E 4\pi r^2

Dove r è il raggio della sfera \Omega, cioè la distanza di P dal centro.

Utilizzando il teorema di Gauss otteniamo:

\Phi_{\Omega}(\overrightarrow{E}) = {Q\over \epsilon_0}

Attenzione però! Quella Q non è più tutta la carica della sfera uniformemente carica, perchè \Omega non contiene più tutta la sfera, ma solo una parte di essa:

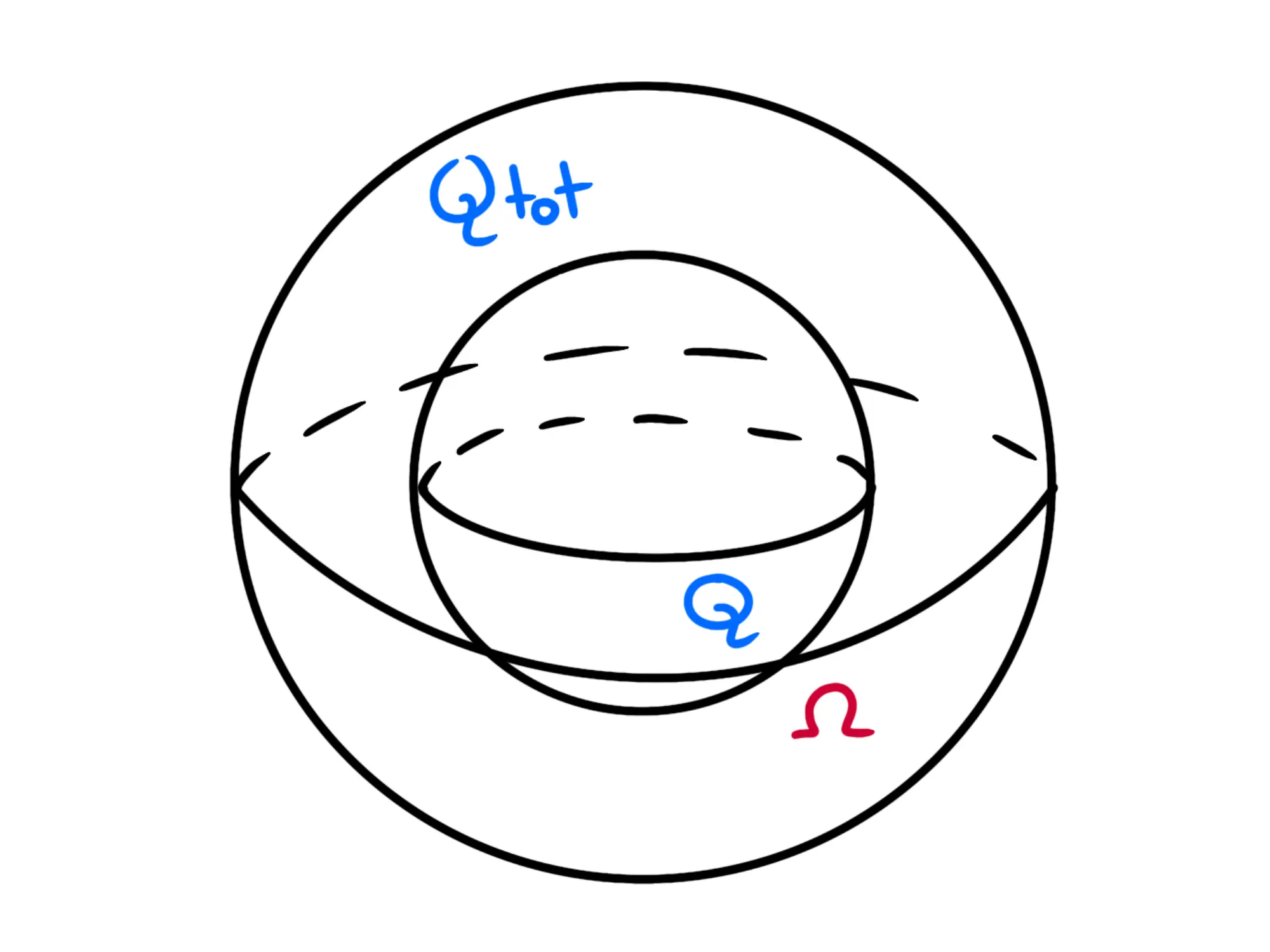
Come calcolare dunque Q? Dobbiamo sfruttare il fatto che la sfera è uniformemente carica. Questo ci dice, infatti, che se chiamiamo \rho (lettera greca che si pronuncia "ro") la densità di carica della sfera, dobbiamo avere:

\rho = {Q\over V}

Siccome la sfera è uniformemente carica, quell'equazione deve essere vera per qualsiasi volume V e carica Q contenuta in esso si prenda della sfera, quindi anche di quello contenuto dentro \Omega.

Dunque deve essere vero che:

\rho = {Q_{\text{tot}}\over V_{\text{tot}}}

e

\rho = {Q \over V_{\Omega}}

Mettendo a confronto le due equazioni, siccome \rho è uguale a \rho , deve anche essere vero che:

{Q\over V_{\Omega}} = {Q_{\text{tot}}\over V_{\text{tot}}}

Q= {V_{\Omega} Q_{\text{tot}}\over V_{\text{tot}}}

Sostituendo dentro la formula del Teorema di Gauss otteniamo:

\Phi_{\Omega}(\overrightarrow{E}) = {{V_{\Omega} Q_{\text{tot}}\over V_{\text{tot}}}\over \epsilon_0}

Se chiamiamo il raggio della sfera carica R, il volume totale V_\text{tot} sarà uguale a {4\over 3}\pi R^3 e il volume contenuto in \Omega sarà uguale a {4\over 3}\pi r^3. Sostituendo otteniamo:

\Phi_{\Omega}(\overrightarrow{E}) = {{{4\over 3}\pi r^3 Q_{\text{tot}}\over {4\over 3}\pi R^3}\over \epsilon_0}

\Phi_{\Omega}(\overrightarrow{E}) = {{r^3 Q_{\text{tot}}\over R^3}\over \epsilon_0}

\Phi_{\Omega}(\overrightarrow{E}) = {r^3 Q_{\text{tot}}\over R^3 \epsilon_0}

Confrontandola con l'altra formula per il flusso che avevamo trovato prima, otteniamo:

E4\pi r^2 = {{r^3 Q_{\text{tot}}\over R^3 \epsilon_0}}

E = {r Q_{\text{tot}}\over 4\pi R^3 \epsilon_0}

E = {Q_{\text{tot}}\over 4\pi R^3 \epsilon_0} r

Come nel caso del capitolo precedente, per risolvere il problema dei segni, basta mettere il modulo a Q_\text{tot}:

E = {|Q_{\text{tot}}|\over 4\pi R^3 \epsilon_0} r

Notiamo che |Q_{\text{tot}}| e R^3 dipendono solo dalla sfera carica e non dal nostro punto P. Solo la sua distanza dal centro r varia al variare di P.

Possiamo dunque trattare quella frazione davanti ad r come una costante, ottenendo E = kr, il che significa che il modulo del campo elettrico E in un punto P all'interno della sfera uniformemente carica è direttamente proporzionale alla sua distanza dal centro r.

Se mettiamo r=0 il punto starà nel centro della sfera e la nostra formula ci dice che in quel caso E=0, dunque al centro della sfera il campo elettrico è nullo. In effetti ha senso, perché al centro, su qualunque direzione, la quantità di particelle che spingono da un lato è la stessa di quella che spingono dal lato opposto, dunque si compensano.

Utilizzando questa formula e quella che avevamo trovato precedentemente nel caso di un punto esterno alla sfera, otteniamo il seguente grafico nel piano r-E:

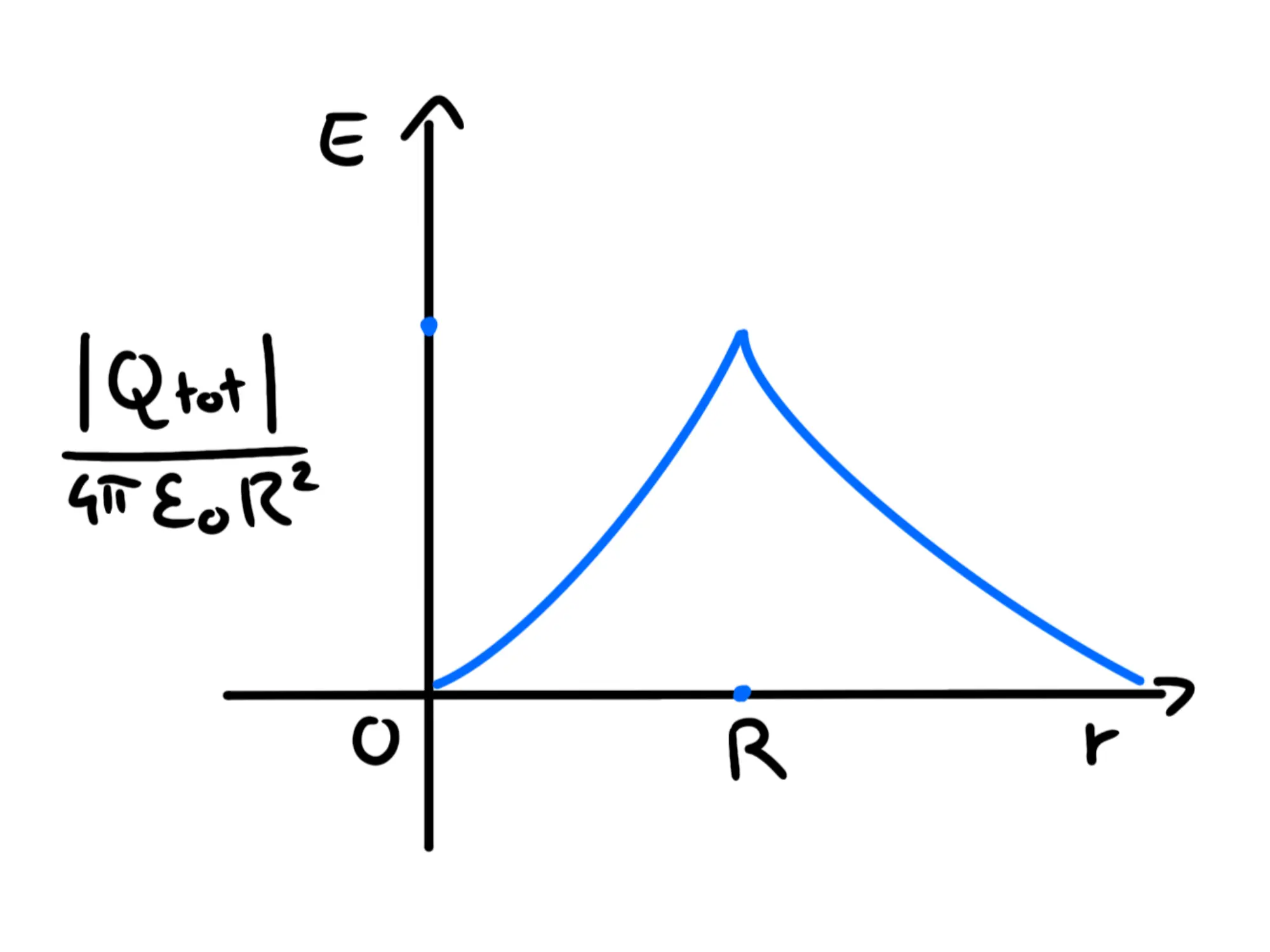
Il massimo sarà, dunque, nel momento di passaggio dalla salita alla discesa, cioè quando cambiamo le formule. Questo succede quando passiamo da dentro alla sfera a fuori alla sfera e il punto di passaggio sarà dunque quando siamo sulla superficie. Infatti questo avviene quando la distanza r dal centro è uguale al raggio R della sfera carica.

Per questo, il campo elettrico di una sfera uniformemente carica è minimo al suo centro, dove vale 0, ed è massimo sulla sua superficie.

Sfera cava uniformemente carica

Cosa succederebbe se la sfera, invece di essere piena, fosse cava? Se ci troviamo fuori alla sfera, notiamo che le formule del flusso del campo elettrico utilizzando il teorema di Gauss e usando la definizione sono uguali a quelle della sfera piena. Dunque otteniamo la stessa formula:

E = {|Q|\over 4\pi\epsilon_0 r^2}

Se però ci troviamo dentro alla sfera, le cose cambiano.

Come sempre, prendiamo un punto P (interno alla sfera) di cui vogliamo calcolare il campo e chiamiamo \Omega la sfera che passa per P e che ha come centro quello della sfera cava:

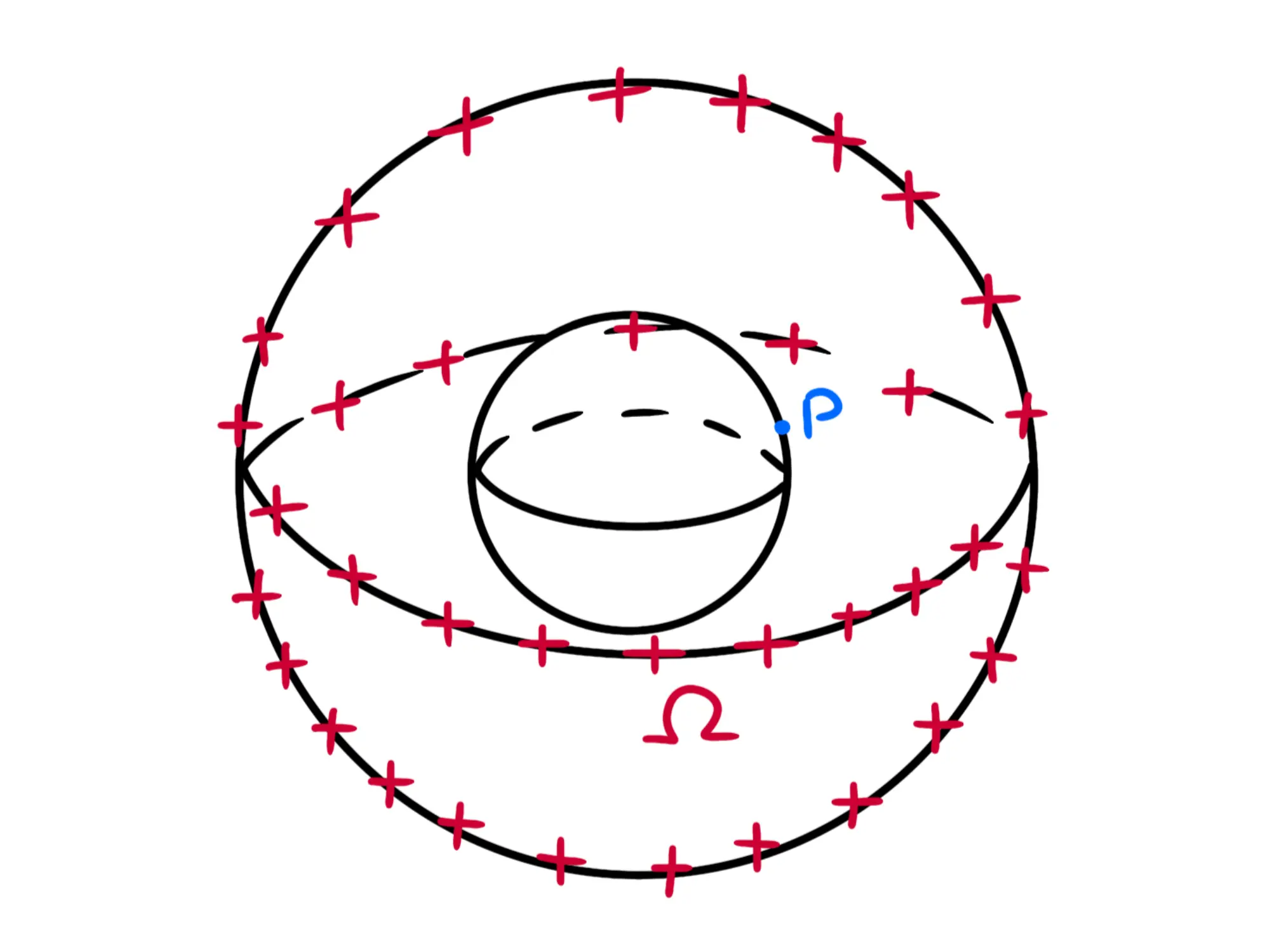
Per le solite ragioni di simmetria i vettori del campo elettrico sulla superficie devono essere perpendicolari a quest'ultima e uguali in modulo.

Usando la definizione, dunque, otteniamo sempre la stessa formula dei casi precedenti:

\Phi_{\Omega}(\overrightarrow{E}) = E4\pi r^2

Utilizzando il teorema di Gauss otteniamo:

\Phi_{\Omega}(\overrightarrow{E}) = {Q\over \epsilon_0}

Però questa volta la sfera è cava! Dunque non c'è nessuna carica contenuta dentro \Omega e quindi Q=0. Questo significa che anche il flusso è uguale a 0. Dobbiamo dunque avere:

E 4 \pi r^2 = 0

E r^2 = 0

A menochè non ci troviamo al centro, r (che ricordiamo essere la distanza del punto dal centro) deve essere diversa da 0 e dunque E=0.

Ma anche se ci troviamo al centro, per le stesse questioni di simmetria della sfera piena, E deve essere uguale a 0.

Dunque, dentro una sfera cava uniformemente carica il campo elettrico è nullo.

Il grafico dell'andamento del modulo di E al variare di r, quindi, questa volta sarà:

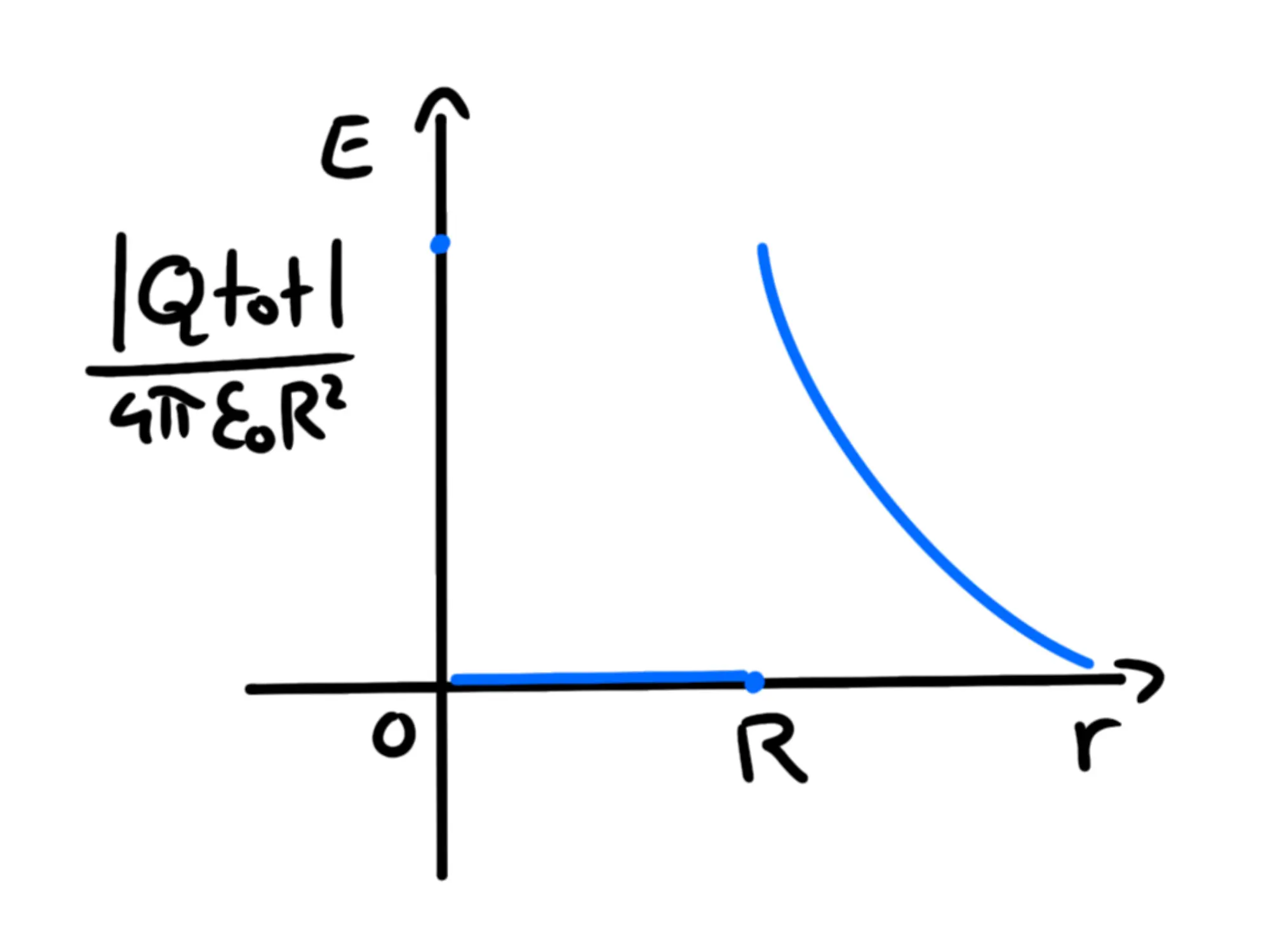
Dove R è il raggio della sfera cava.