Retta e piano uniformemente carichi

Retta infinita carica uniformemente

Prendiamo tante cariche uguali e sistemiamole su una riga:

Pensiamo ora di metterne infinite e schematizziamo il tutto usando una retta:

La carica totale della retta, essendo infinita, sarà infinita, quindi più che guardare alla carica ci interessa la densità di carica \lambda, cioè quanta carica ci sta in un metro di retta.

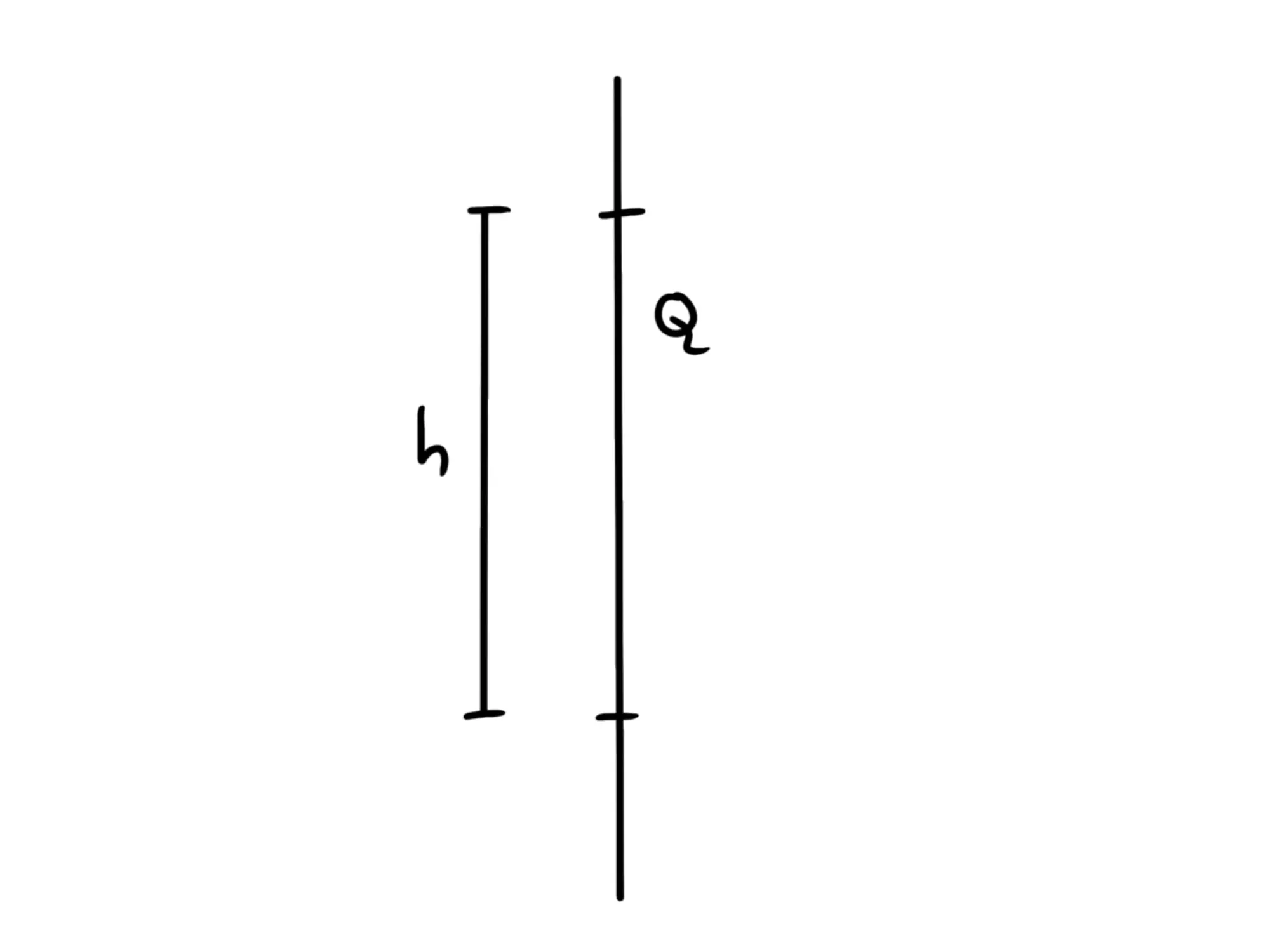
Per calcolarla ci basterà prendere un segmento di lunghezzza h della corda, prendere la carica Q contenuta in questo pezzetto e dividerlo per h:

\lambda = {Q\over h}

Quello che noi vogliamo fare, ora, è calcolare quanto vale il campo elettrico in un punto P:

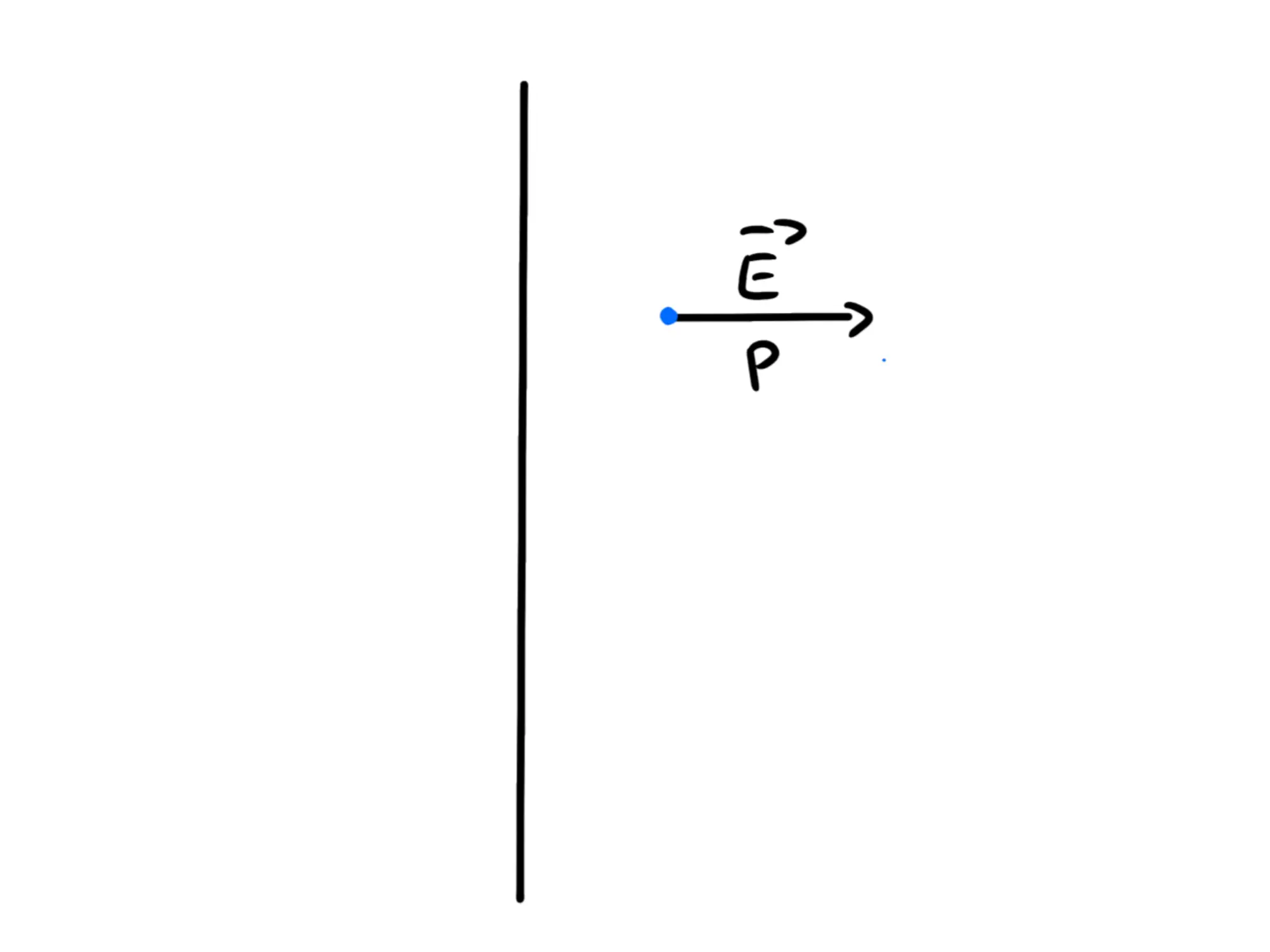
Iniziamo facendo qualche considerazione di tipo geometrico:

Se noi prendiamo la retta e la spostiamo un po' verso l'alto, siccome è infinita, non cambierà niente. Questo significa che la retta è simmetrica rispetto a taslazione verso l'alto o il basso.

Prendiamo quindi due punti uno sopra all'altro e supponiamo per assurdo che i loro campi elettrici siano diversi:

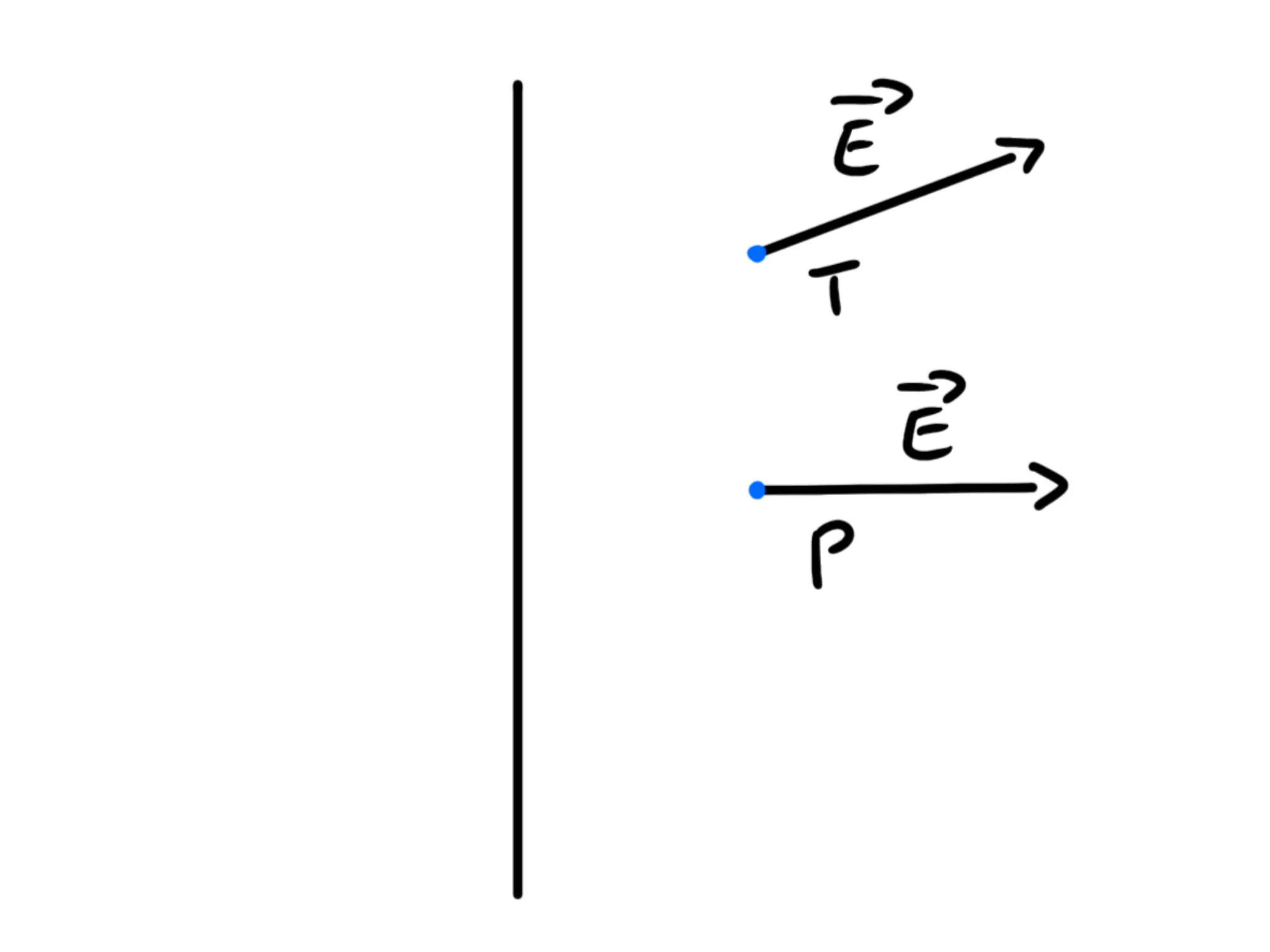
Se prendiamo la retta e il punto T e li muoviamo nello spazio, siccome non ci sono altre cariche, non cambia niente. Quindi fissiamo P e spostiamo la retta e T verso il basso in maniera che P e T coincidano:

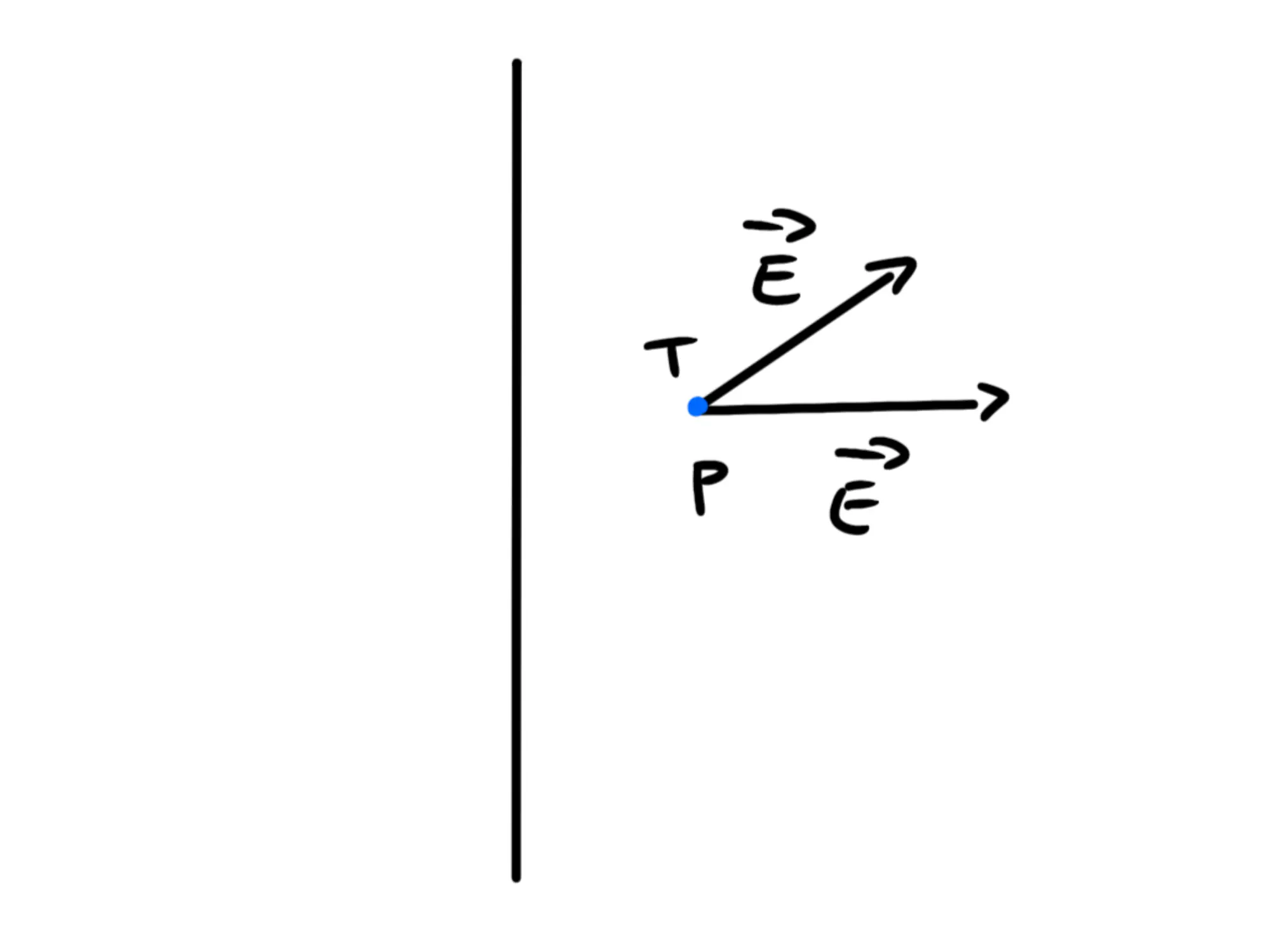
Ma avevamo detto che la retta era simmetrica rispetto a traslazioni verso il basso o l'alto, dunque la retta che avevamo prima è esattamente uguale a quella che abbiamo adesso, perciò come è possibile che nel punto P ci possano essere due campi elettrici diversi? E' impossibile e dunque il campo elettrico in T e in P deve essere uguale.

Notiamo ora che la retta è simmetrica anche rispetto a rotazioni su sè stessa:

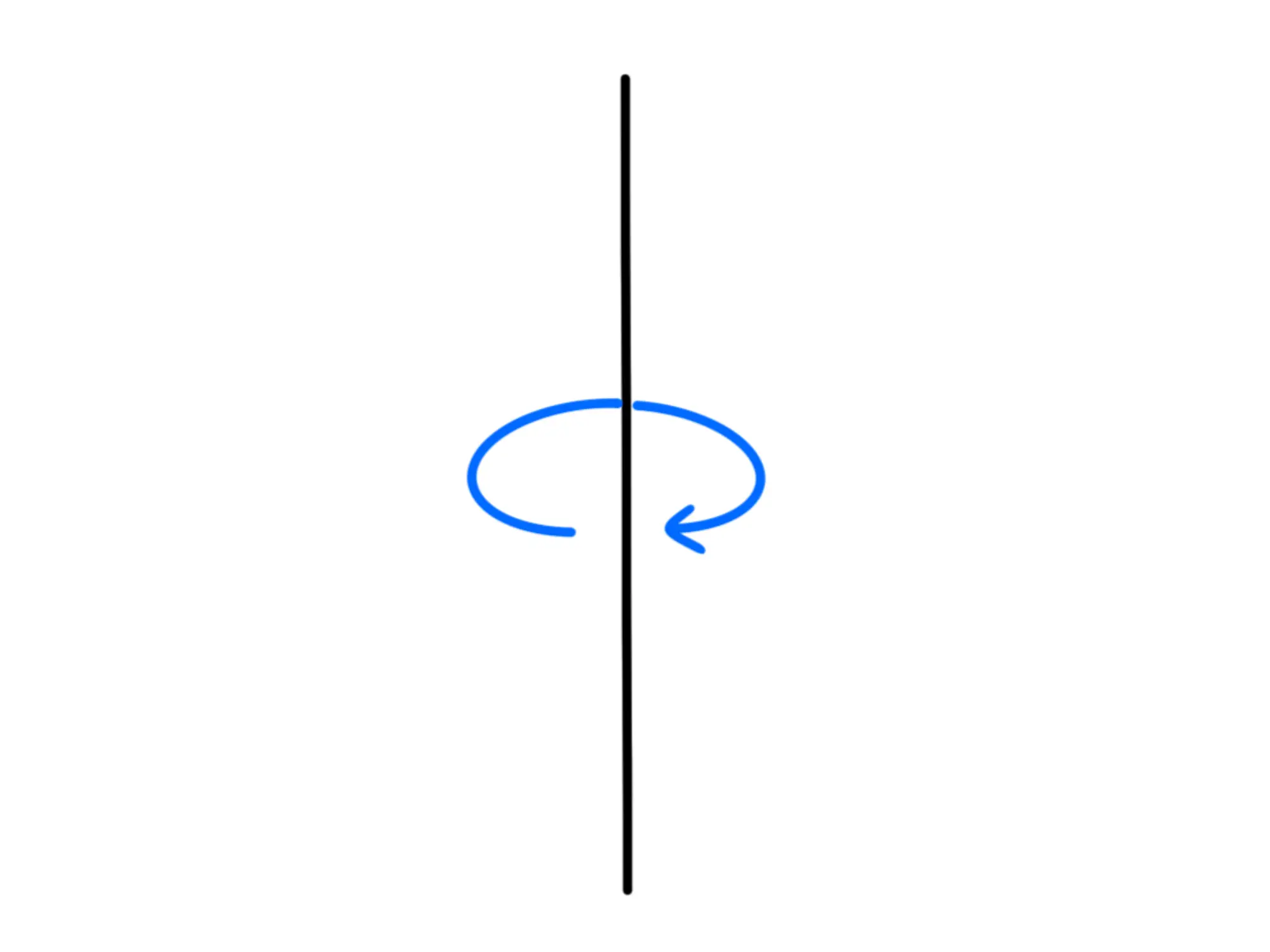
Dunque, per lo stesso ragionamento di prima, se prendiamo tutti i punti su una circonferenza con centro sulla retta, i campi elettrici devono essere messi a raggiera, in maniera che ruotando si sovrappongano perfettamente:

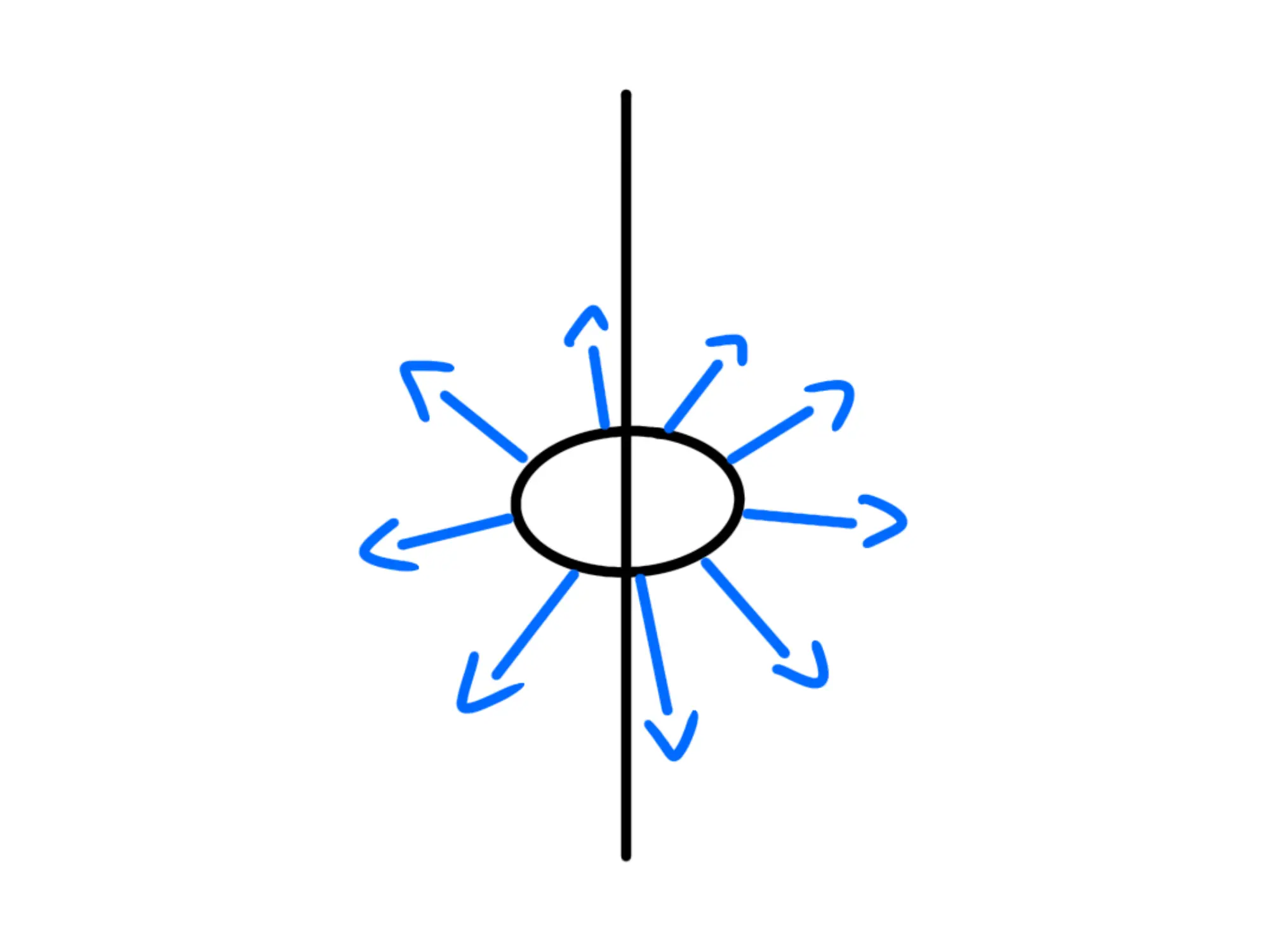
Notiamo pure che quindi i vettori del campo elettrico sono sempre perpendicolari alla circonferenza.

Questo è quello che succede se la retta è caricata positivamente. Se la sua carica è negativa, sarà tutto uguale tranne il verso, che, invece di puntare via, punterà verso la retta:

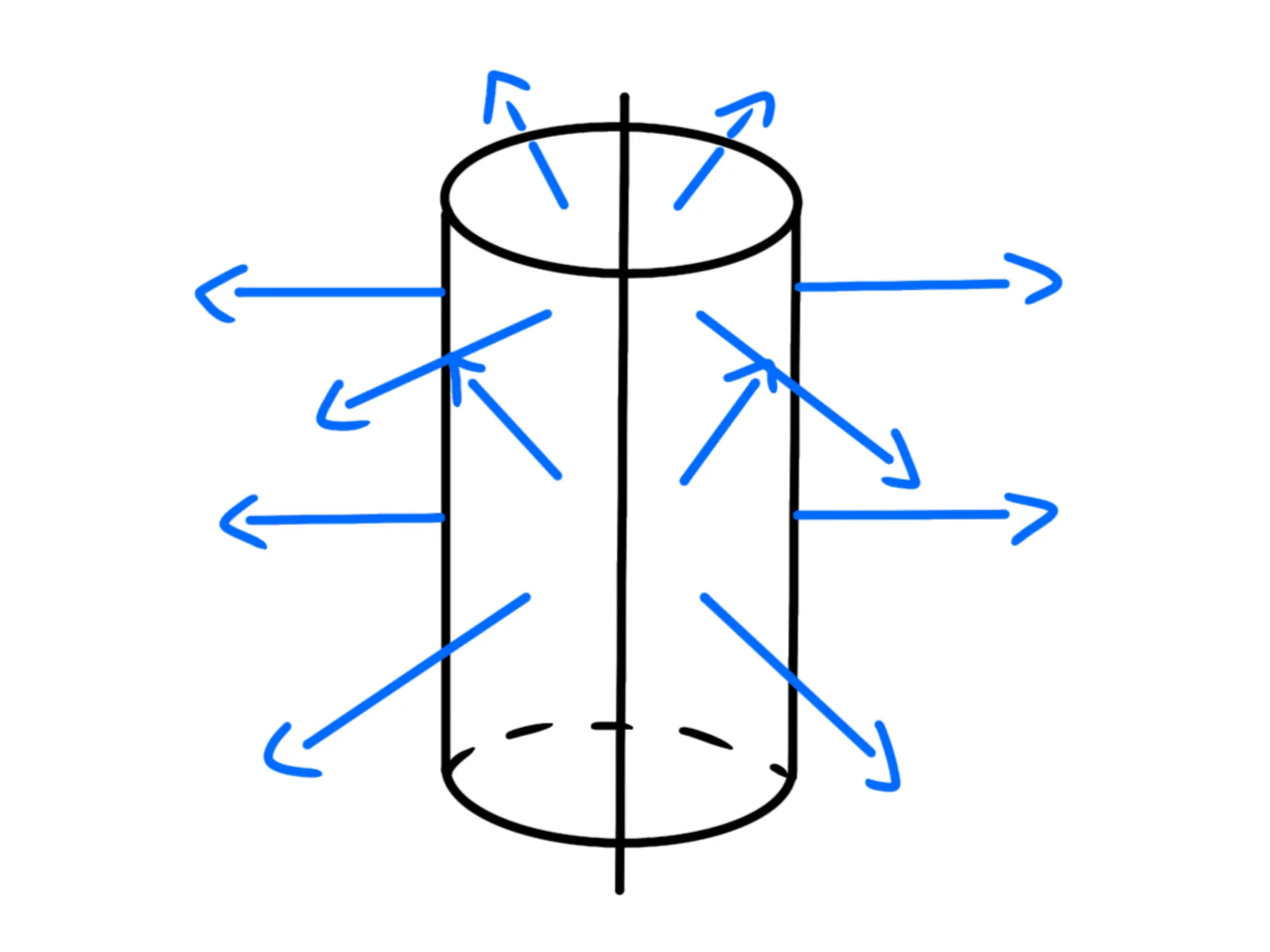
Combinando le informazioni ottenute dalle due simmetrie, otteniamo che il campo elettrico lungo la superficie laterale di un cilindro è sempre uguale in modulo e il suo vettore è sempre perpendicolare al cilindro:

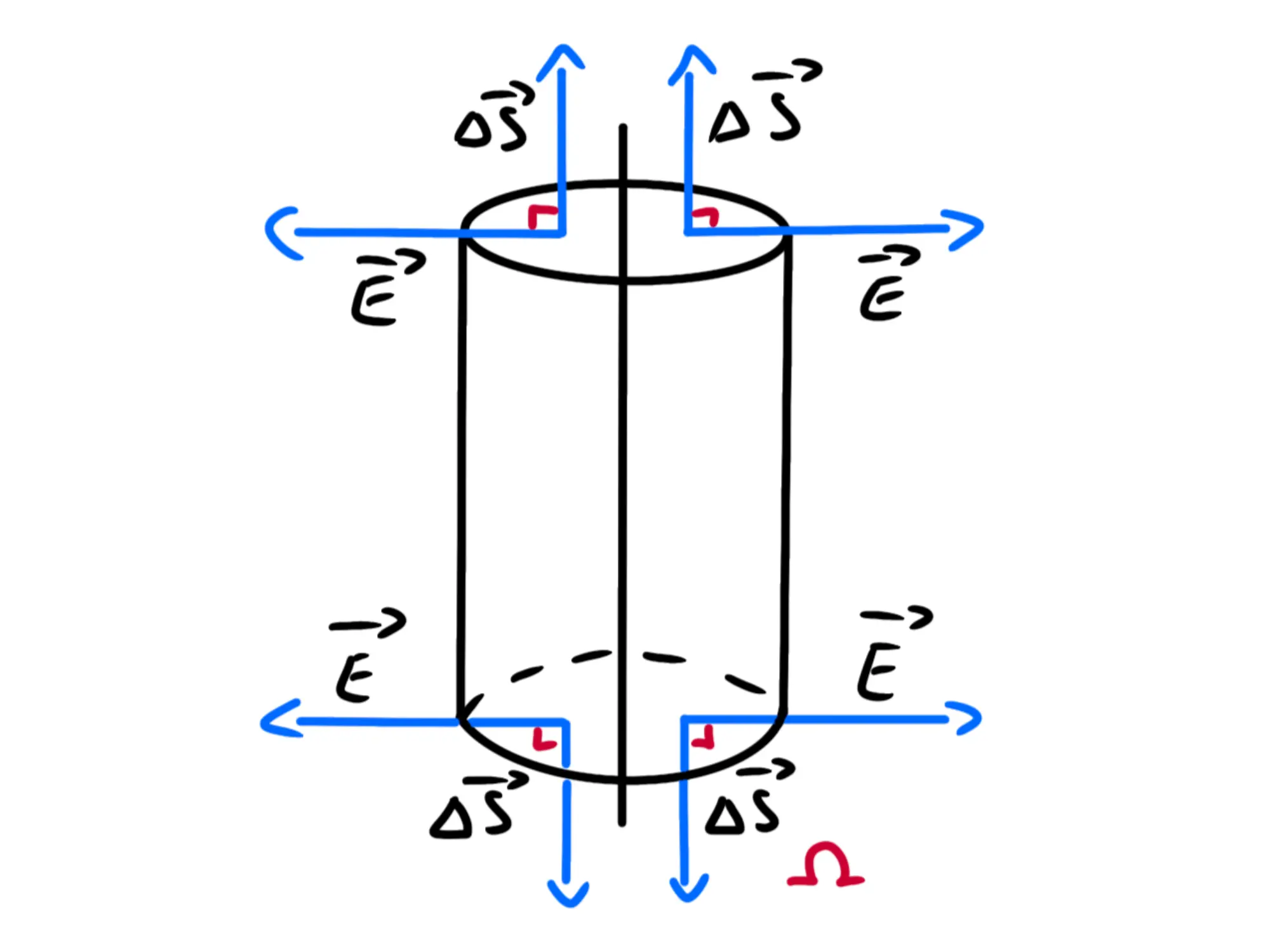
Sembra dunque molto comodo lavorare con questa tipologia di cilindri. Proviamo quindi a calcolare il flusso del campo elettrico su questo cilindro (che ora chiameremo \Omega) in due modi, con la sua definizione e con il teorema di Gauss, e poi confrontiamo i risultati:

Iniziamo dall'appliccare il metodo più facile, cioè il teorema di Gauss.

Siccome il cilindro \Omega è una superficie chiusa, se chiamiamo Q la carica contentua nel pezzetto di retta dentro al cilindro, abbiamo:

\Phi_{\Omega}(\overrightarrow{E}) = {Q\over \epsilon_0}

Ora usiamo invece la definizione del flusso del campo elettrico:

Iniziamo notando che il flusso passante per la basi del cilindro è 0 perché il vettore del campo elettrico e il vettore superficie sono perpendicolari e dunque il loro prodotto scalare è 0:

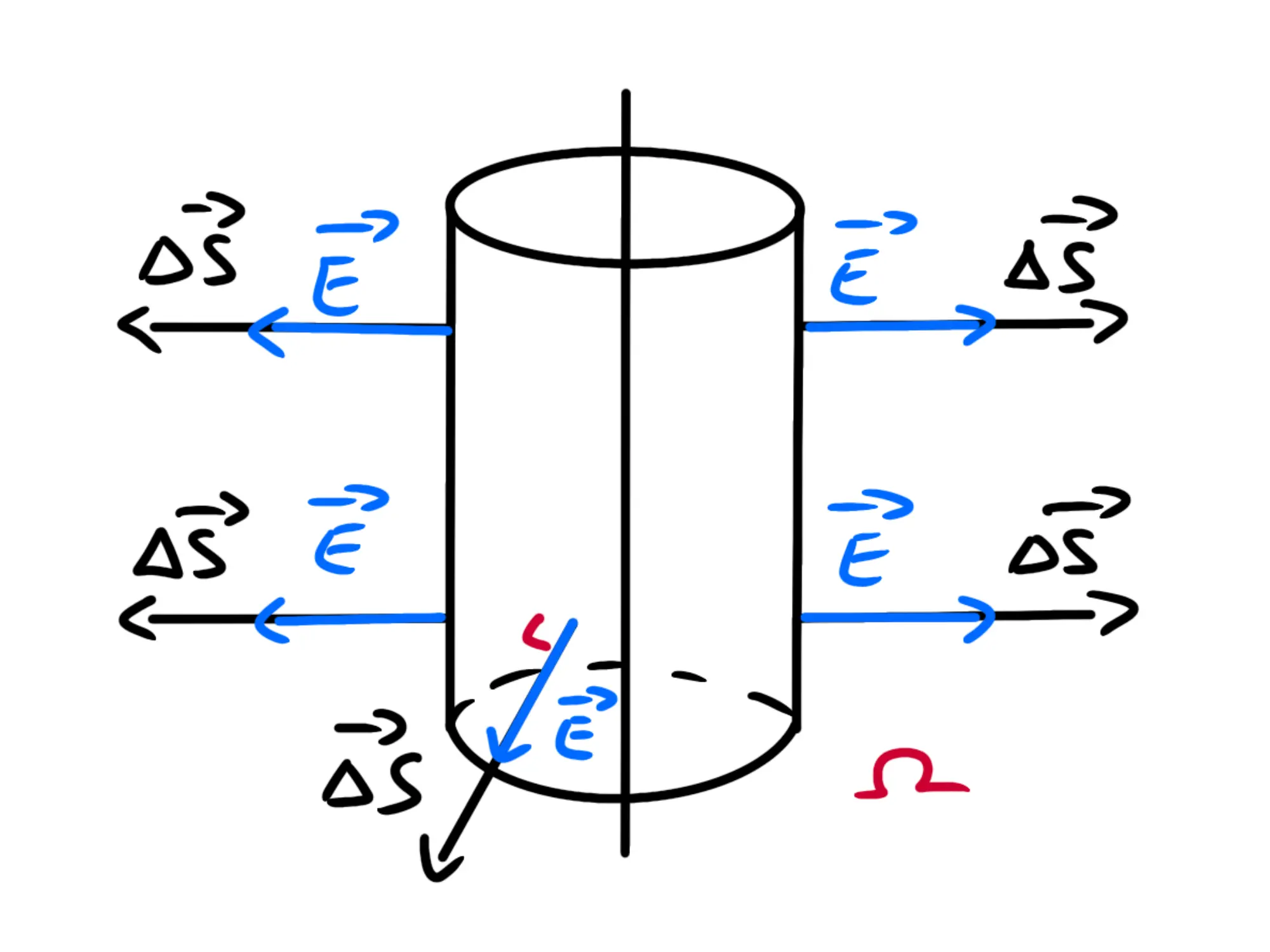
Quindi dobbiamo solo calcolare il flusso passante per la superficie laterale. Avevamo detto prima che il campo elettrico era perpendicolare alla superficie laterale del cilindro, dunque deve essere parallelo al suo vettore superficie:

Dunque dobbiamo avere \overrightarrow{E}\cdot \Delta \overrightarrow{S} = E \Delta S. Ricordiamo poi che E è costante su tutta la superficie laterale del cilindro. Dunque dobbiamo avere:

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N \overrightarrow{E_i} \cdot \Delta \overrightarrow{S_i}

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N E_i \cdot \Delta S_i

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N E \cdot \Delta S_i

\Phi_{\Omega}(\overrightarrow{E}) =E \cdot \sum_{i=1}^N \Delta S_i

La somma di tutti i moduli dei vettori superficie ci da la superficie laterale del cilidro S_l. Dunque:

\Phi_{\Omega}(\overrightarrow{E}) = E S_l

La superficie laterale di un cilindro si calcola come la sua circonferenza per l'altezza, quindi se ha raggio r e altezza h abbiamo:

S_l = 2\pi r h

Quindi:

\Phi_{\Omega}(\overrightarrow{E}) = 2\pi E r h

Ed avevamo trovato prima, usando il teorema di Gauss, che \Phi_{\Omega}(\overrightarrow{E}) ={Q\over \epsilon_0} . Dunque, confrontando le due equazioni, otteniamo:

2E\pi r h = {Q\over \epsilon_0}

E = {Q \over 2 \pi \epsilon_0 r h}

Ed avevamo detto all'inizio che la carica Q contenuta in un pezzetto della retta di lunghezza h divisa per h era uguale, per definizione, alla densità di carica \lambda della retta. Perciò il risultato finale è:

E = {\lambda \over 2 \pi \epsilon_0 r}

Ovviamente, se al posto di stare nel vuoto ci troviamo in un qualsiasi mezzo, ci basterà sostituire \epsilon_0 con la costante dielettrica assoluta del mezzo \epsilon:

E = {\lambda \over 2 \pi \epsilon r}

Quindi sappiamo che i vettori del campo elettrico generato da una retta infinita uniformemente carica sono disposti a raggiera ed hanno modulo {\lambda \over 2 \pi \epsilon r}, dove r è la distanza dalla retta (il raggio del cilindro).

Ora vediamo se al posto di una retta abbiamo un piano:

Piano infinito carico uniformemente

Ora prendiamo delle cariche uguali q e mettiamole su un piano:

Ora pensiamo di mettere infinite cariche su questo piano in maniera da ricoprirlo tutto quanto in maniera uniforme. Per semplificare rappresentiamo quello che abbiamo creato con un comune piano:

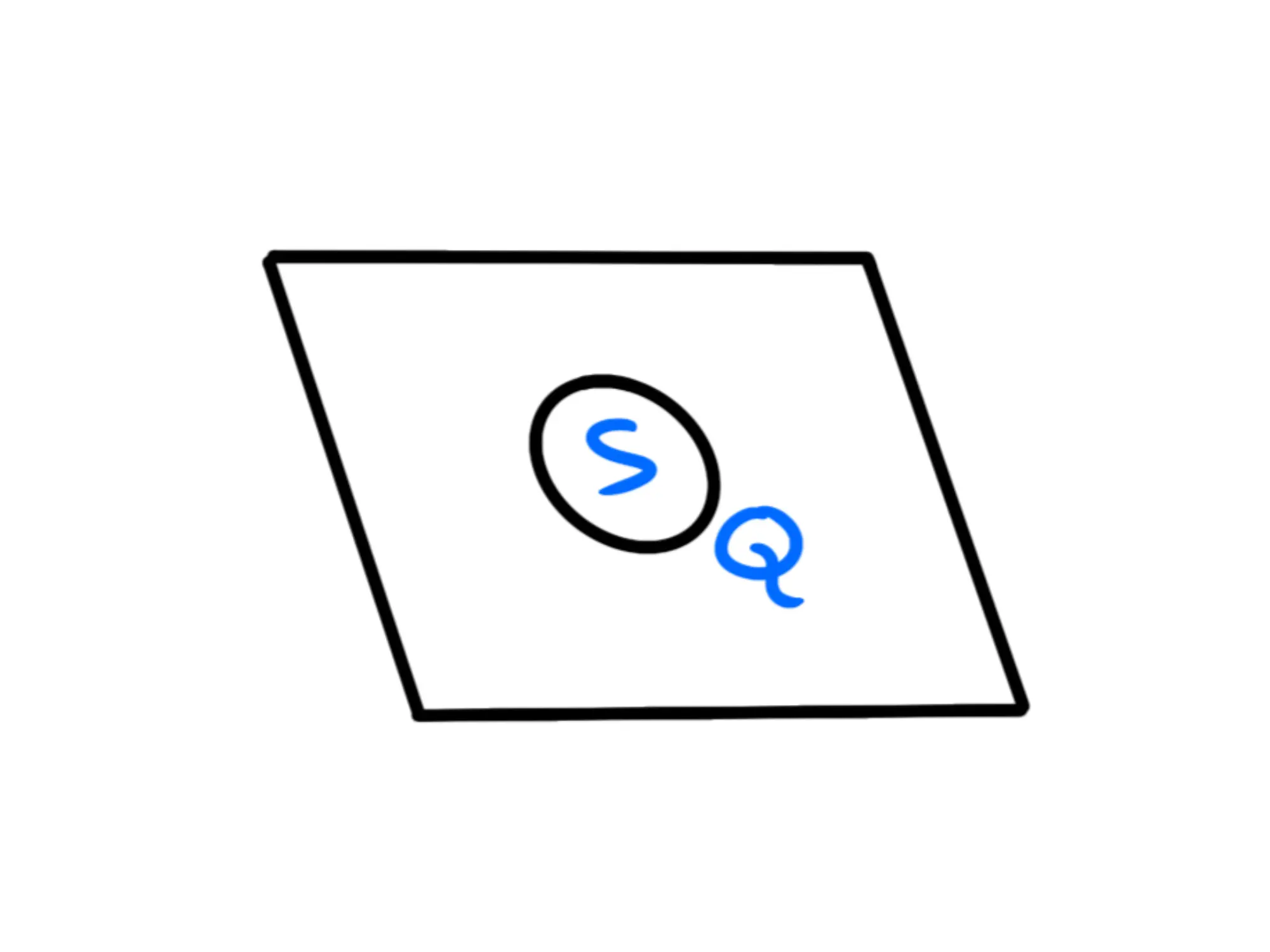
Come nel caso della retta, il piano avrà una carica infinita, quindi guarderemo alla densità di carica \sigma (sigma) del piano, cioè al rapporto tra quanta carica Q è contenuta in un pezzetto del piano e l'area S di quest'ultimo:

\sigma = {Q \over S}

Anche in questo caso iniziamo con delle considerazioni geometriche:

Notiamo che se spostiamo il piano lungo i suoi assi, essendo infinito, non cambia niente:

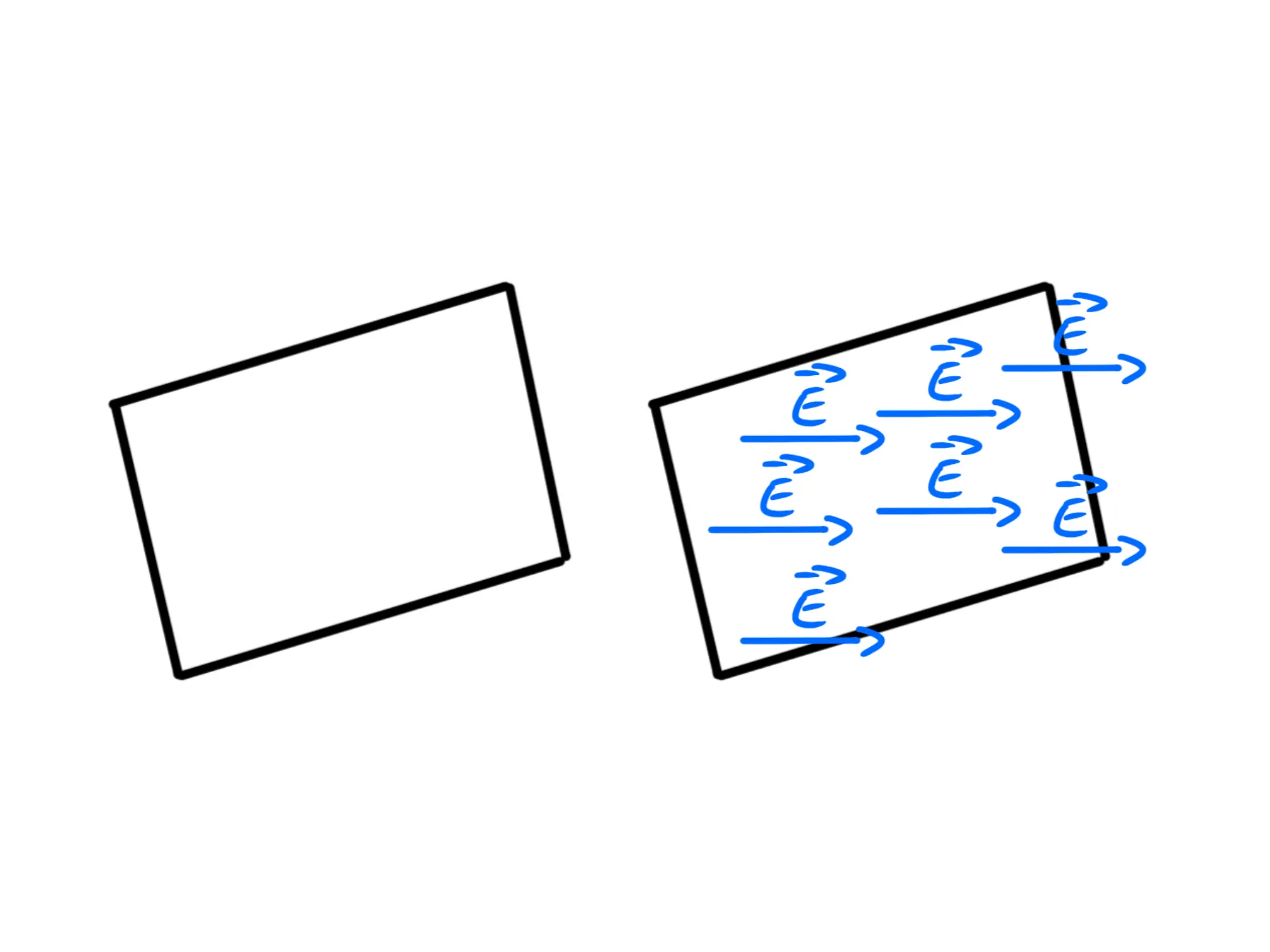
Dunque, per lo stesso ragionamento che avevamo fatto per la retta, il campo elettrico deve essere uguale in tutti i punti equidistanti dal piano, cioè in tutti i punti che stanno su un piano parallelo a quello carico:

Notiamo che anche ruotando il piano intorno a sè stesso non cambia niente:

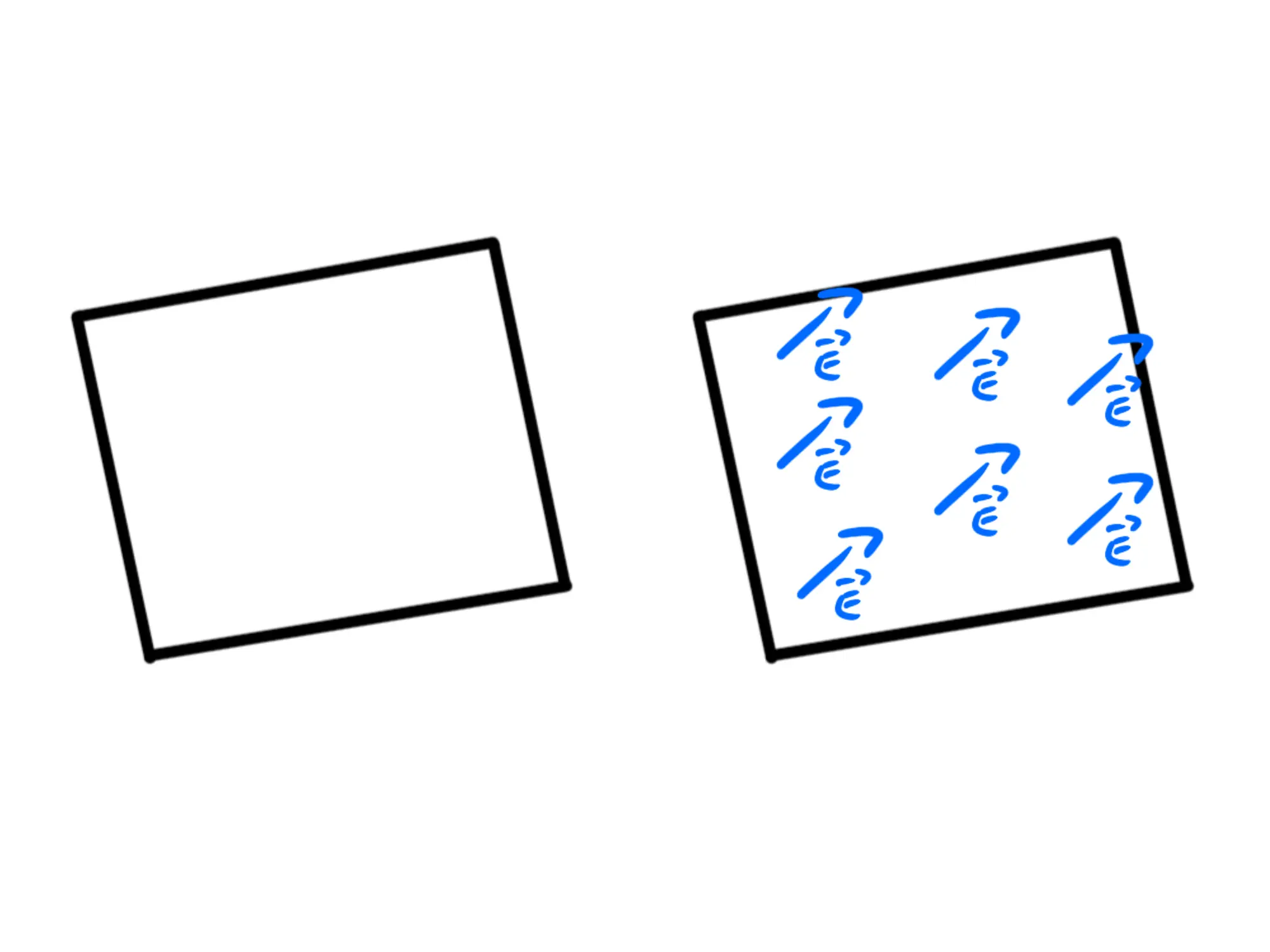
Dunque se i vettori non fossero perpendicolari al piano, quando ruotiamo il tutto, cambierebbero la direzione e questo sarebbe assurdo perché il piano carico è sempre lo stesso.

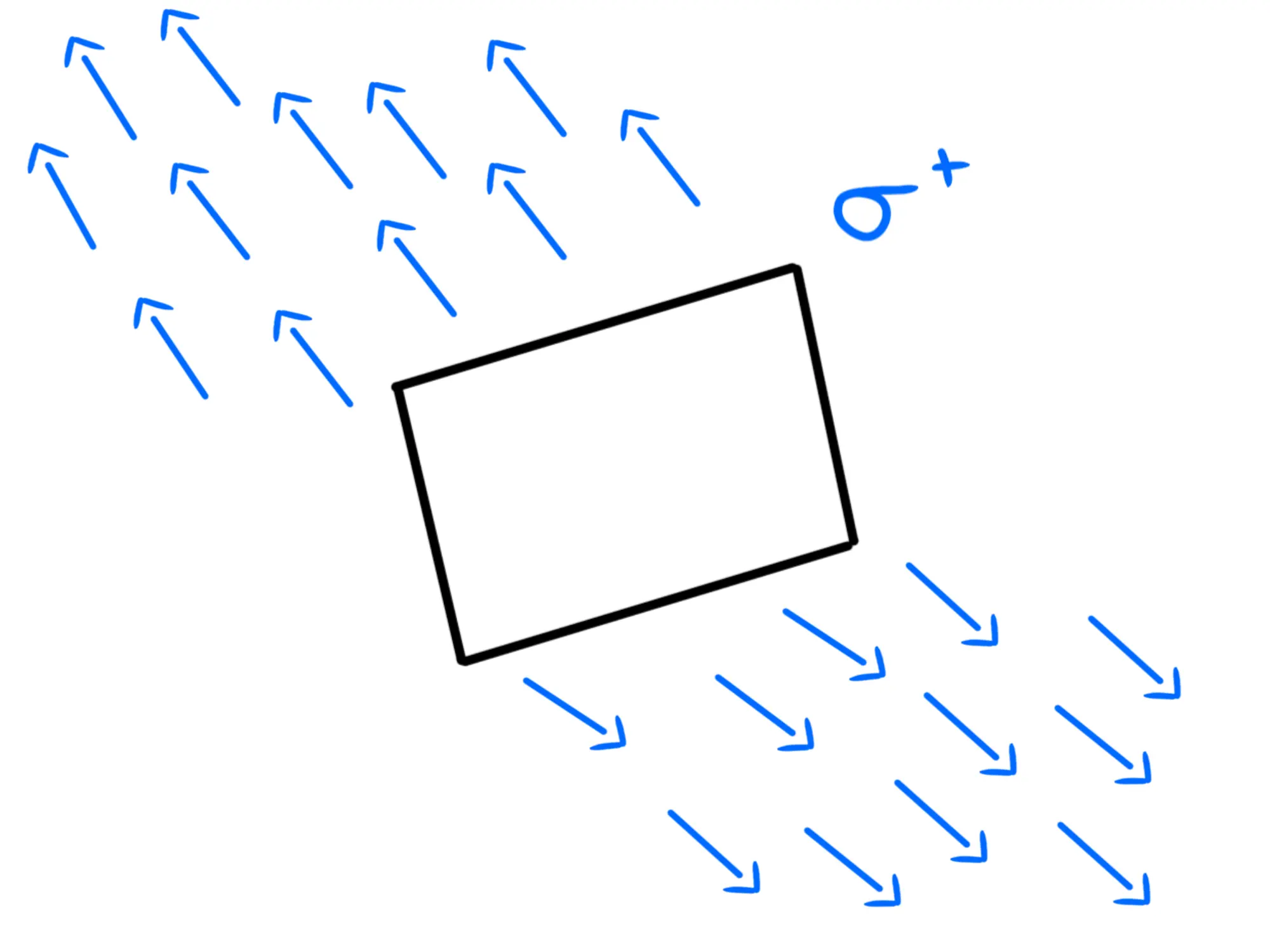
Dunque tutti i vettori sono perpendicolari al piano:

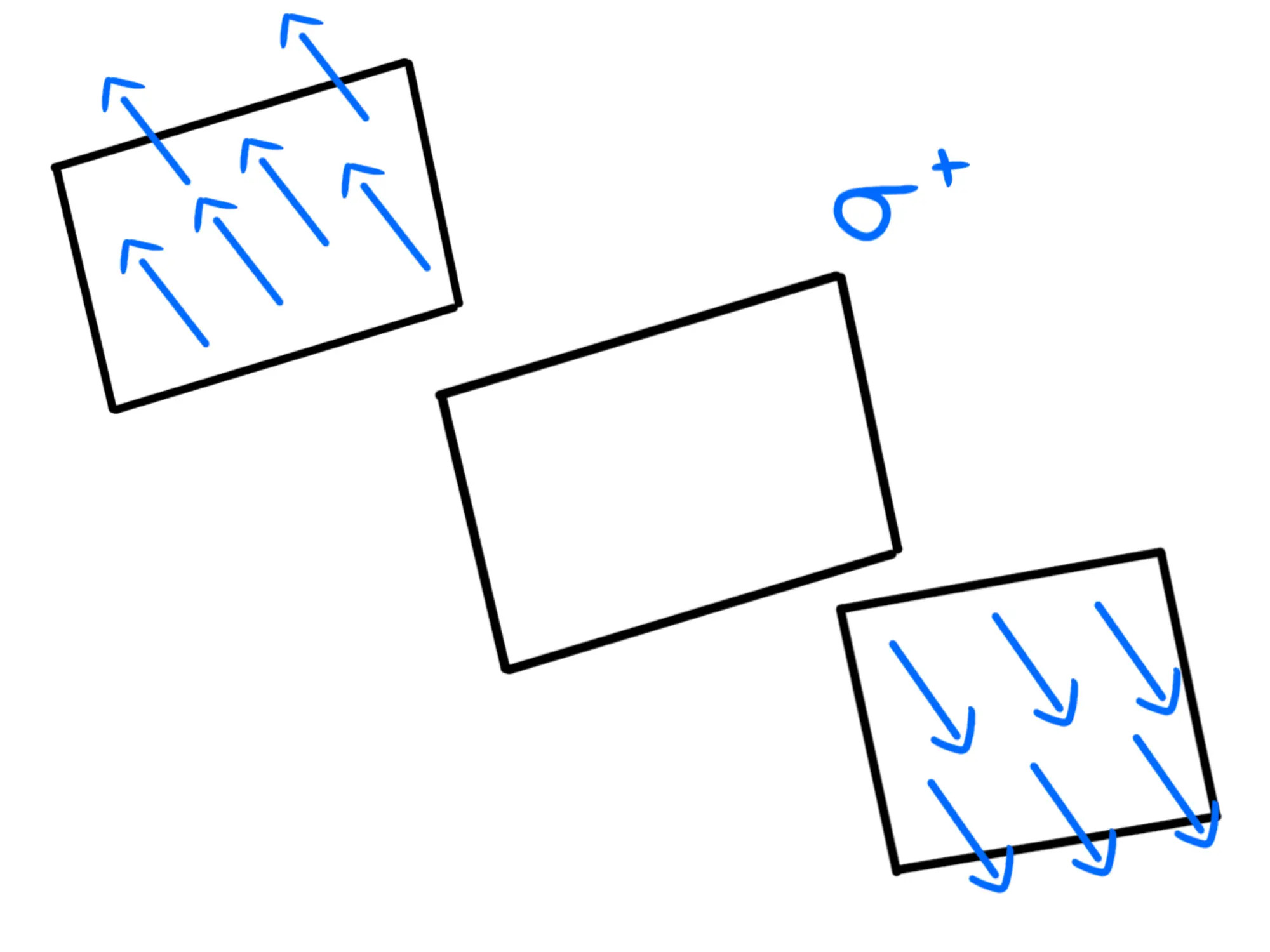
Il verso? Se la densità di carica è positiva, dovranno allontanarsi dal piano, se è negativa gli punteranno contro:

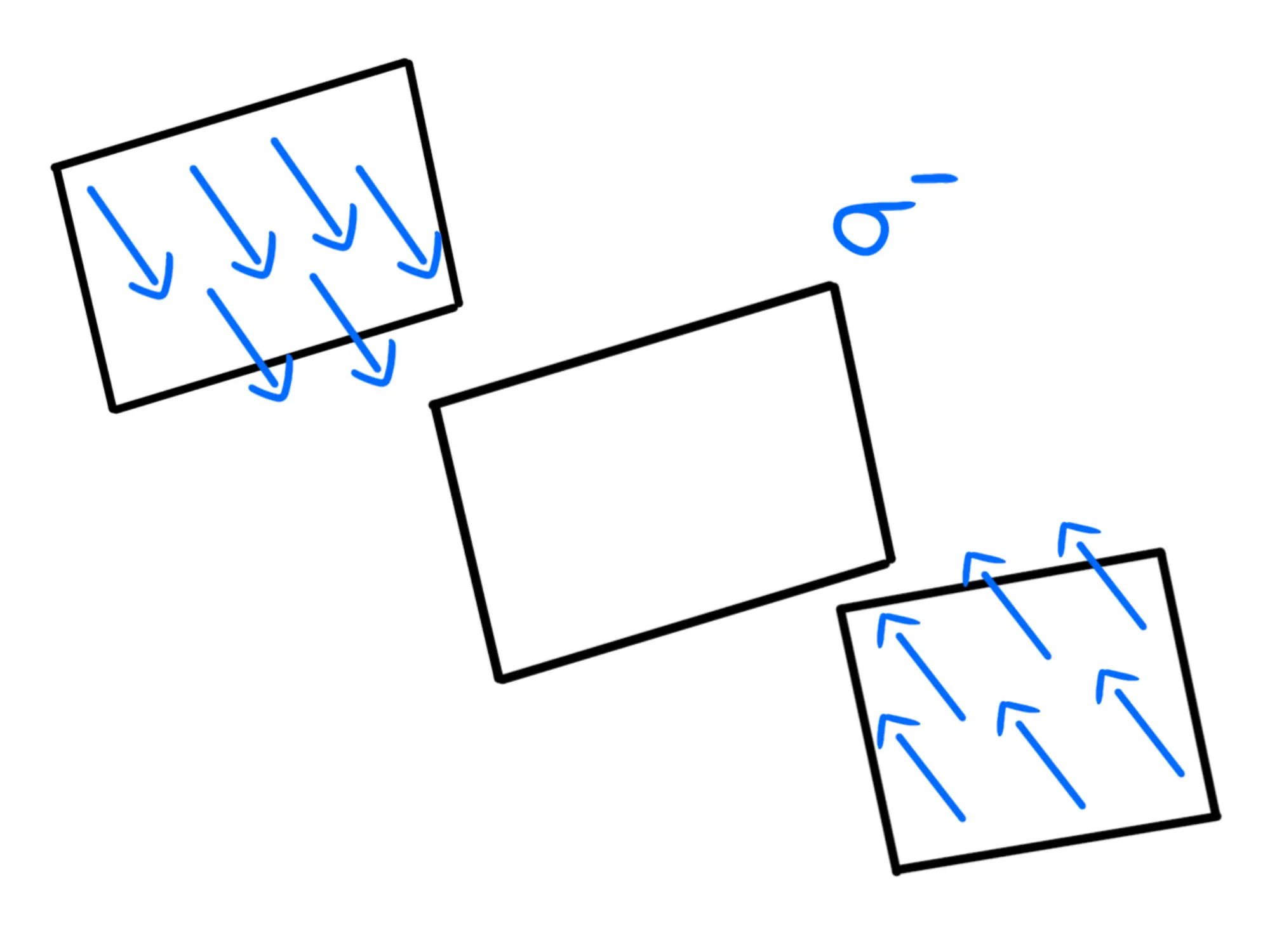
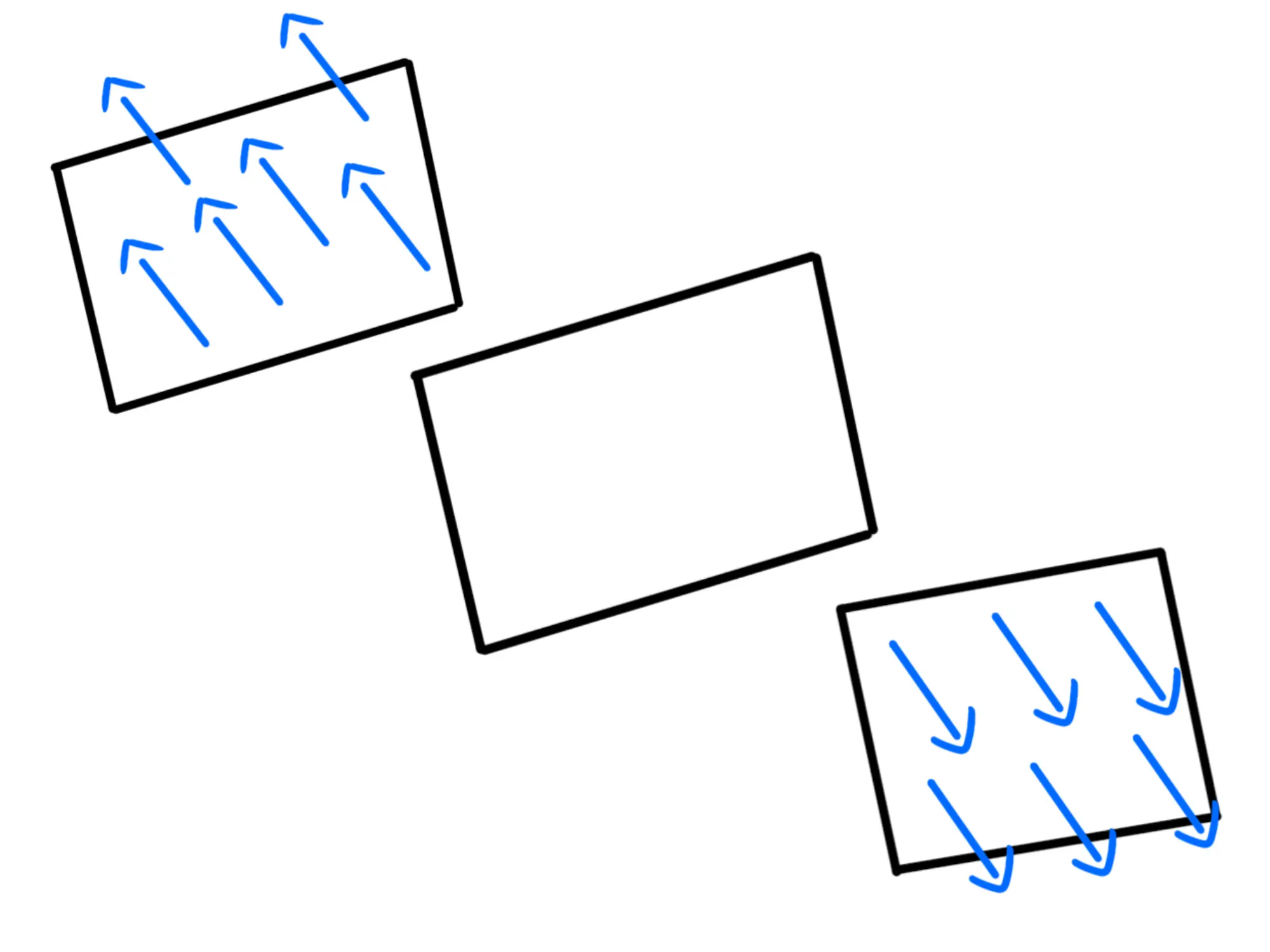
Prendiamo quindi ora due piani paralleli al piano carico equidistanti da esso:

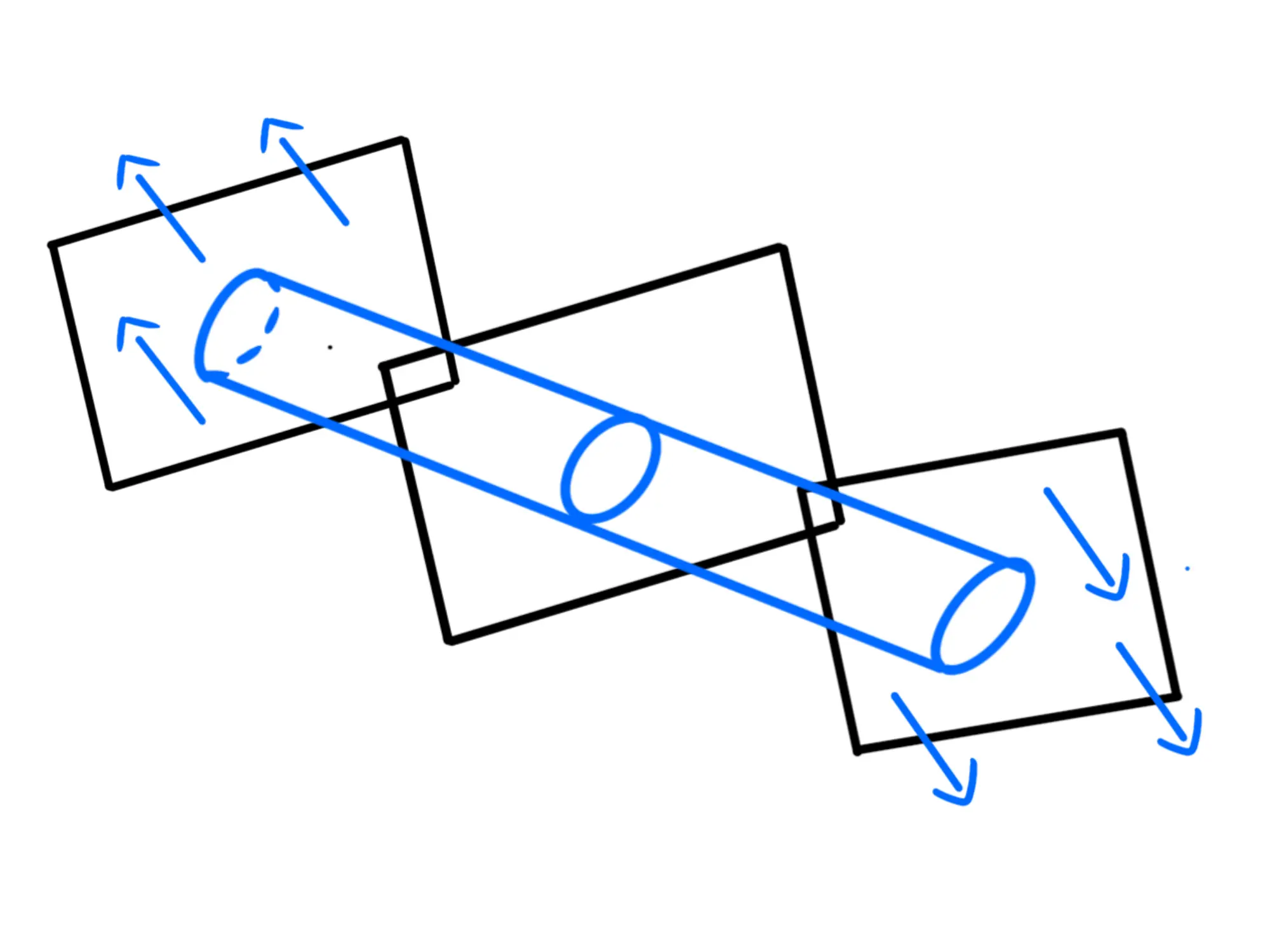
Notiamo che il modulo del campo elettrico è costante lungo entrambi i piani ed è sempre perpendicolare ai piani.

Conosciamo già la direzione e il verso del campo elettrico, ci manca solo il modulo. Per trovarlo possiamo fare lo stesso procedimento della retta: calcoliamo il flusso del campo elettrico in due modi diversi e li confrontiamo.

Prendiamo perciò due cerchi uguali sui due piani alla stessa altezza e colleghiamoli, creando così un cilindro con le basi parallele al piano carico e la superficie laterale perpendicolare ad esso:

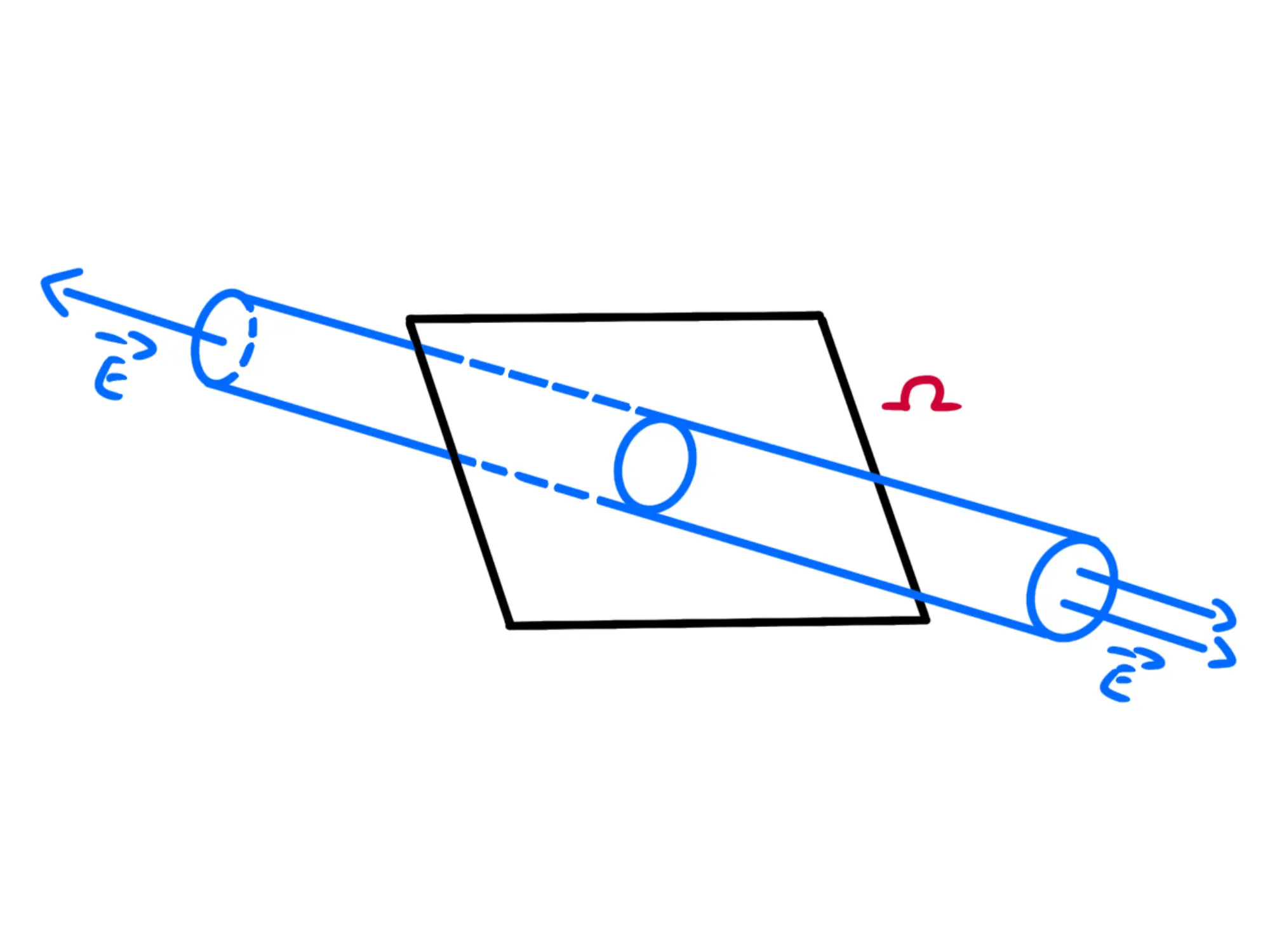
Per semplificare prendiamo solo le basi del cilindro e leviamo il resto dei due piani e chiamiamo il cilindro \Omega:

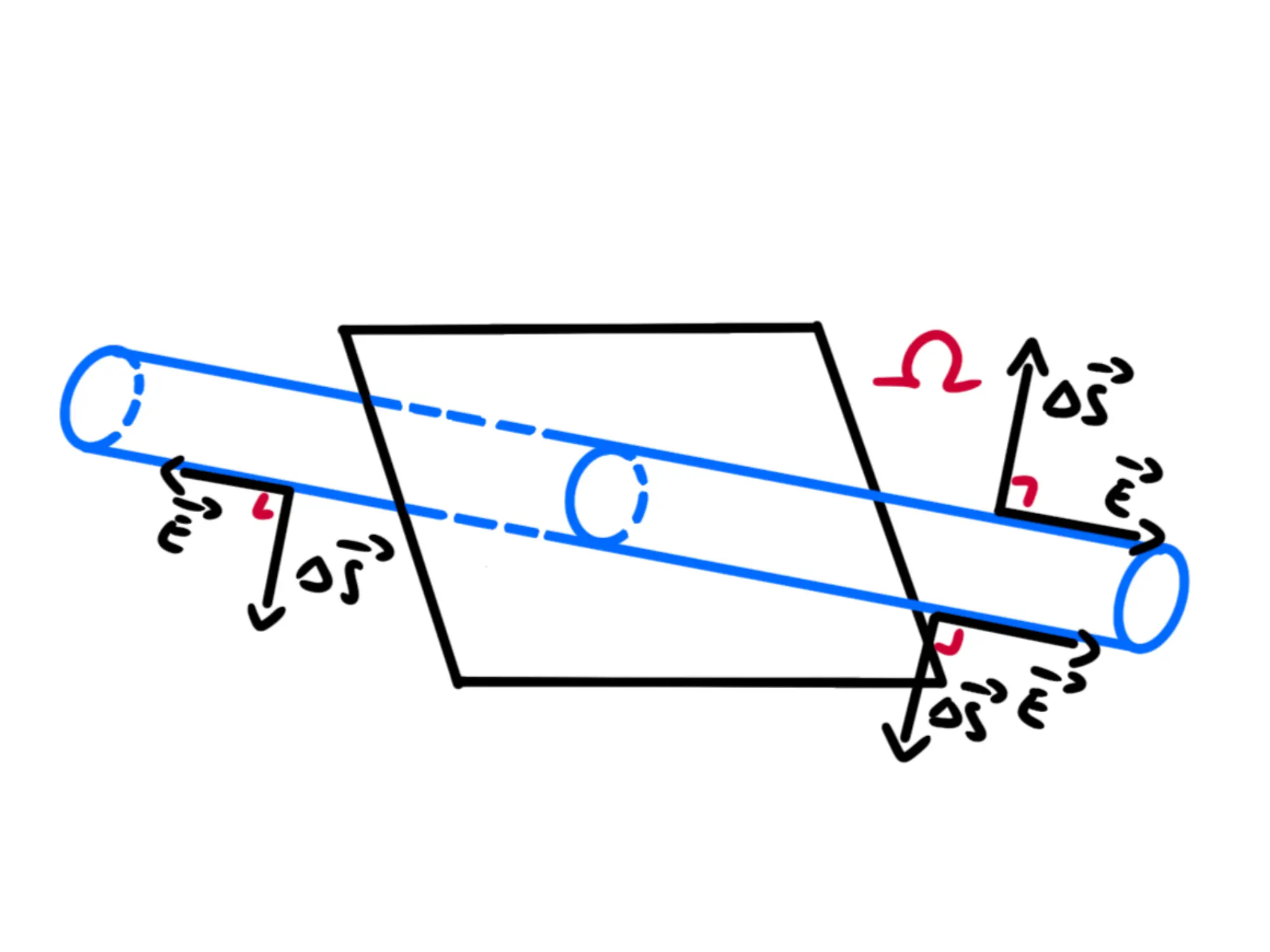
Calcoliamo ora il flusso che passa per \Omega usando il teorema di Gauss:

Siccome il cilindro è una superficie chiusa, se chiamiamo Q la carica contenuta nel pezzetto nel piano dentro al cilindro, per il teorema di Gauss dobbiamo avere:

\Phi_{\Omega}(\overrightarrow{E}) = {Q\over \epsilon_0}

Ora calcoliamolo usando la definzione:

Abbiamo detto che il campo elettrico è perpendicolare al piano. Anche la superficie laterale del cilindro è perpendicolare al piano, dunque il vettore superficie di quest'ultima deve essere perpendicolare ad \overrightarrow{E}:

Quindi il prodotto scalare tra \overrightarrow{E} e \Delta \overrightarrow{S} è uguale a 0 e dunque il flusso passante per la superficie laterale è uguale a 0.

Dobbiamo quindi calcolare solo quello delle basi. Siccome qua invece avremo che \overrightarrow{E} ed \Delta \overrightarrow{S} sono paralleli, dobbiamo avere \overrightarrow{E} \cdot \Delta \overrightarrow{S} = E \Delta S e il modulo di \overrightarrow{E} è costante su entrambe le basi, dunque dobbiamo avere:

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N \overrightarrow{E_i} \cdot \Delta \overrightarrow{S_i}

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N E_i \cdot \Delta S_i

\Phi_{\Omega}(\overrightarrow{E}) = \sum_{i=1}^N E \cdot \Delta S_i

\Phi_{\Omega}(\overrightarrow{E}) = E \cdot \sum_{i=1}^N \Delta S_i

La somma di tutti i vettori superficie delle due basi ci da l'area delle due basi del cilidro.

Se chiamiamo S_b l'area di una sola delle superfici di base, siccome ne abbiamo due, dobbiamo avere:

\Phi_{\Omega}(\overrightarrow{E}) = E \cdot 2S_b

Ricordandoci che avevamo ottenuto anche che \Phi_{\Omega}(\overrightarrow{E}) ={Q\over \epsilon_0}, possiamo mettere a confronto le due equazioni ed ottenere:

2 E S_b = {Q\over \epsilon _0}

E = {Q \over 2 \epsilon_0 S_b}

Notiamo che l'area della superficie di base del cilindro è uguale all'area del pezzetto di piano contenuto dentro il cilindro. Dunque, per definizione, Q\over S_b è uguale alla densità di carica \sigma. Sostituendo otteniamo il risultato finale:

E = {\sigma \over 2 \epsilon_0}

Notiamo dunque che il modulo del campo elettrico non dipende nemmeno dalla distanza dal piano, quindi deve essere uguale in tutti i punti dello spazio. Questo significa che otteniamo un campo elettrico uniforme, cioè in realtà due, uno a destra del piano che punta verso destra e uno a sinistra del piano che punta verso sinistra, (se la carica è positiva, sennò è il contrario):

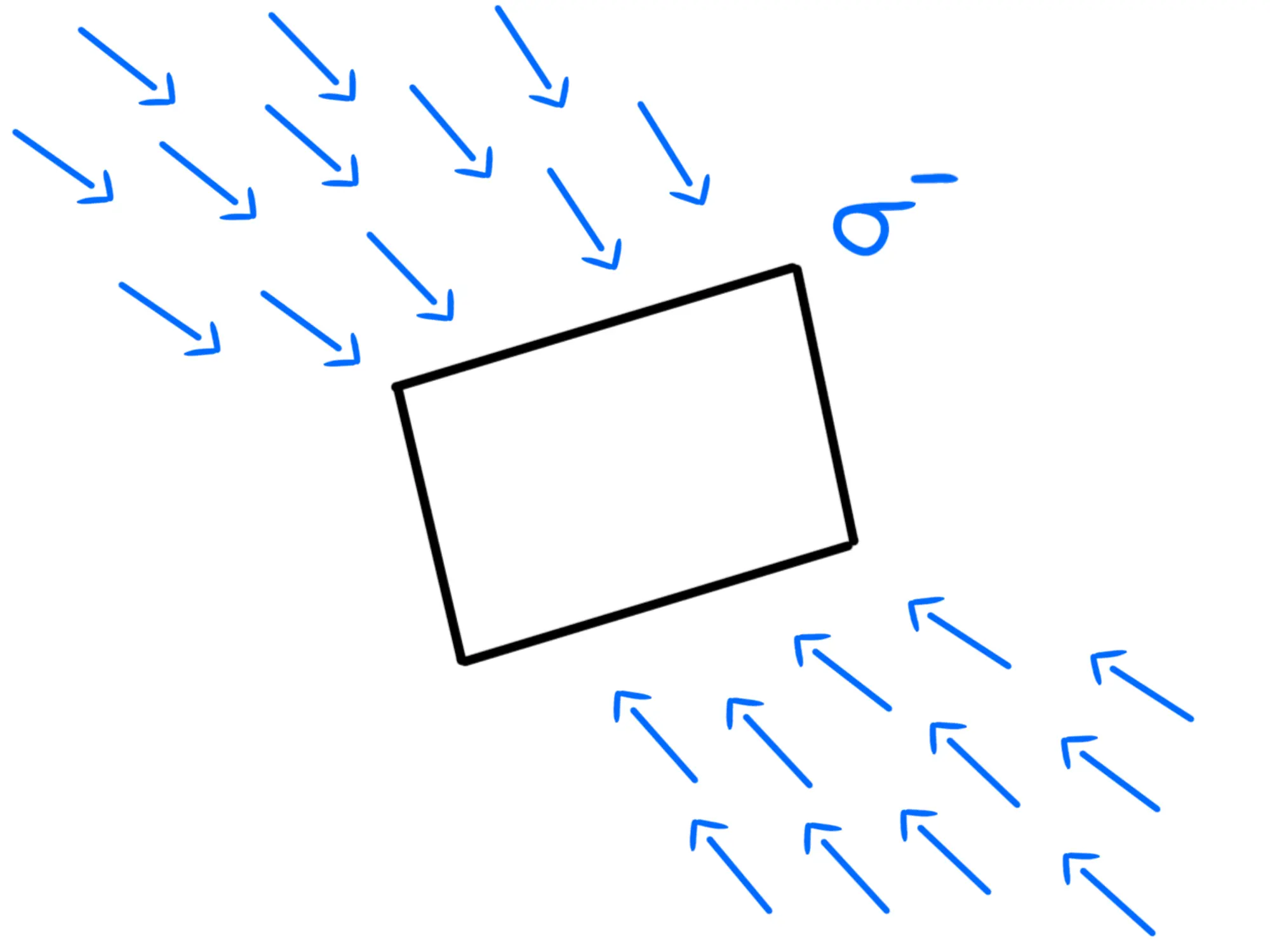
Concludiamo la lezione facendovi notare come questo dimostri l'utilità di usare il campo elettrico e il suo flusso.

Se adesso vogliamo sapere la forza che viene applicata ad una carica nello spazio in presenza di una retta infinita carica uniformemente o un piano carico uniformemente, ci basta prendere il campo elettrico, che conosciamo, e moltiplicarlo per la carica della particella. Se non avessimo usato il campo elettrico e il suo flusso sarebbe stato molto più complicato calcolare la forza che viene applicata a quella particella.