La regola di Ruffini

Cos’è la regola di Ruffini?

La regola di Ruffini è una tecnica di scomposizione dei polinomi ed è stata introdotta dal matematico Paolo Ruffini. Risulta utile in quanto riesce a scomporre polinomi non scomponibili con le altre tecniche che abbiamo visto in una lezione apposita (cliccate qui per accedervi).

Questo metodo di scomposizione si basa sul Teorema di Ruffini, il cui enunciato è “Un polinomio è divisibile per un binomio del tipo x-a soltanto se scambiando la sua incognita con l’opposto del termine noto del divisore viene annullato”.

In questa lezione ci limiteremo a spiegare come e quando applicare la regola e non dimostreremo il teorema in sé, chiarito questo possiamo procedere.

Quando usare Ruffini

Dato che usare la regola di Ruffini è il metodo più lento per scomporre un polinomio, consigliamo di provare prima tutte le altre tecniche di scomposizione. Quindi, se il grado del polinomio è minore o uguale a 3, molto probabilmente è scomponibile anche in altri modi.

Se ci si trova davanti un polinomio di grado elevato e non si riesce a ricondurlo a gradi inferiori usando, ad esempio, il raccoglimento totale, allora è conveniente procedere con Ruffini in quanto è facile e sicuro.

Come applicare Ruffini

La prima cosa che bisogna fare con il nostro polinomio è trovare un numero che lo annulli, cioè un numero che se sostituito all’incognita faccia venire 0.

Si potrebbero provare tutti i numeri reali ma fortunatamente sappiamo che deve per forza essere un divisore dell’ultimo termine del polinomio, ovvero quello non moltiplicato per la nostra incognita.

Esempio:

7x^2+4x-3 \longrightarrow \pm1 e \pm 3 -proviamo le opzioni e scopriamo che -1 è accettabile

Ora, trovato il nostro numero, sappiamo che il nostro polinomio sarà divisibile per x più il reciproco di questo numero che nel nostro caso è 1.

Potremmo dunque affermare che (x+1) \cdot (...) = 7x^3+4x-3

Fatto questo non ci resta che svolgere la divisione e scoprire quale polinomio si ottiene se si divide il primo per x+1.

Per fare questo disegniamo una tabella, e scriviamo dopo la prima colonna, ordinati in base al grado, i coefficienti numerici dei termini del polinomio di partenza e l’ultimo coefficiente aldilà della seconda linea verticale:

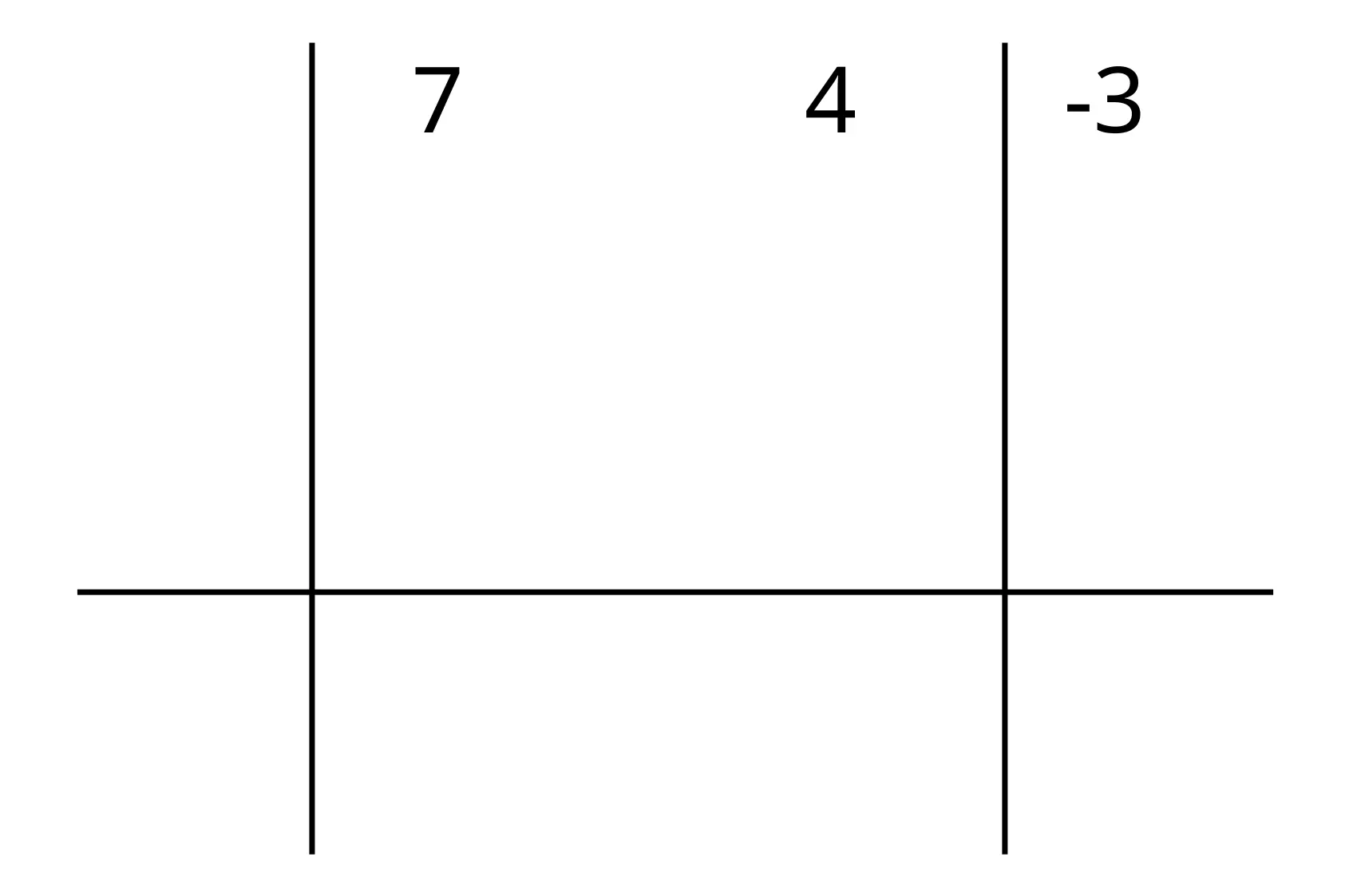
Poi procediamo a scrivere il numero che annulla il polinomio a sinistra sopra la linea orizzontale e iniziamo a fare i calcoli:

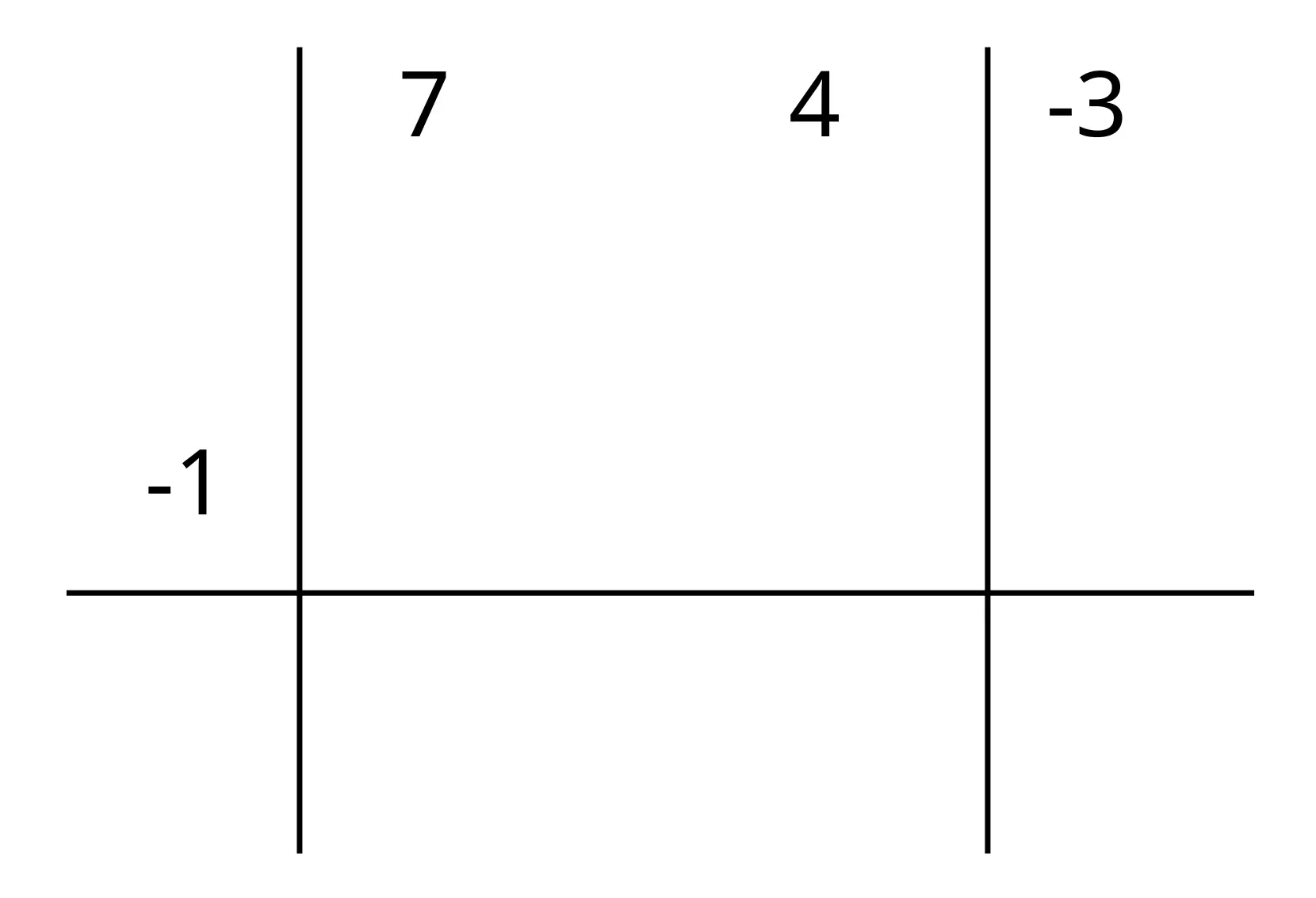
Per svolgere i calcoli si segue questo procedimento: si parte dal primo coefficiente che abbiamo scritto in alto e lo si trascrive sotto la linea orizzontale, ora si svolge la moltiplicazione tra questo numero e il numero scritto a sinistra della linea verticale e il risultato lo si scrive sotto il secondo coefficiente, si somma il secondo coefficiente al risultato della moltiplicazione di prima e si scrive il risultato sotto la linea.

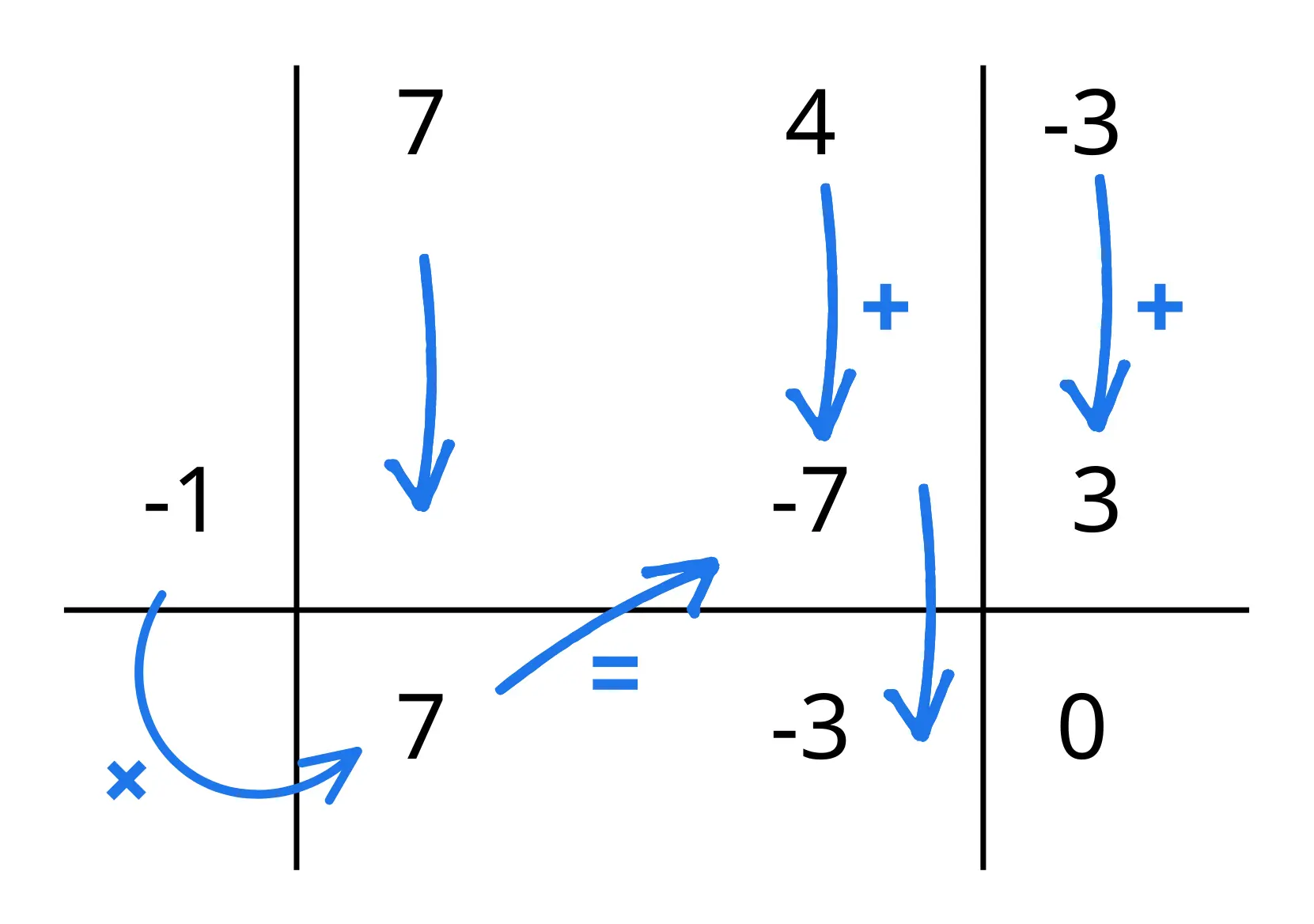
Si ripete il procedimento fino all’ultimo coefficiente e eseguendo la somma di questo con il numero sottostante si ottiene 0 (se tutto è stato fatto correttamente).

Il polinomio risultante avrà per coefficienti i numeri scritti sotto la linea orizzontale (notare che i coefficienti sono uno in meno perché il risultato è di un grado inferiore al polinomio di partenza).

Il risultato della nostra scomposizione sarà quindi (x+1)(7x-3).