Poliedri
Di seguito analizzeremo i poliedri.
Cosa sono i poliedri?
I poliedri sono solidi la cui superficie è formata interamente da poligoni. Quindi, ad esempio, un cubo è un poliedro:
E anche questo qua è un poliedro:
Però una sfera non è un poliedro:
E anche un cilindro non lo è:
Perchè le loro superfici non sono formate interamente da poligoni.
Ogni poligono da cui i poliedri sono formati viene chiamata faccia.
I lati dei poligoni vengono chiamati spigoli.
I vertici dei poligono vengono sempre chiamati vertici.
Un segmento che congiunge due vertici non consecutivi del poliedro è detto diagonale.
Se la diagonale congiunge due vertici della stessa faccia, è detta di superficie, altrimenti è detta interna:
La definizione di poliedro è molto generale, per questo effettuiamo ulteriori classificazioni:
Poliedri convessi e concavi
La definizione di convessità per i poliedri è la stessa esatta di quella di convessità per i poligoni che abbiamo visto in un'altra lezione:
Un poliedro è detto convesso se, presi due punti qualsiasi dentro di esso, il segmento che congiunge questi due punti giace interamente all'interno di esso.
Se un poliedro non è convesso, allora è concavo.
Quindi un cubo è un poliedro convesso, ma un poliedro con "spuntoni" che fuoriescono o con "rientranze", come il secondo che abbiamo visto, è concavo. Solitamente ci interessano di più i poliedri convessi e raramente vedremo poliedri concavi.
Passiamo quindi alla prossima classificazione:
Poliedri regolari ed irregolari
Un poliedro è detto regolare se le sue facce sono formate da poligoni regolari e sono tutte uguali.
Se un poligono non è regolare, allora è irregolare.
La definizione di poliedro regolare potrebbe sembrare ancora abbastanza generale, ma in realtà esistono solo 5 poliedri che soddisfano i suoi requisiti.
Essi vengono talvolta chiamati solidi platonici perché Platone li studiò e sono:
Il tetraedro regolare:
L'esaedro regolare (il cubo):
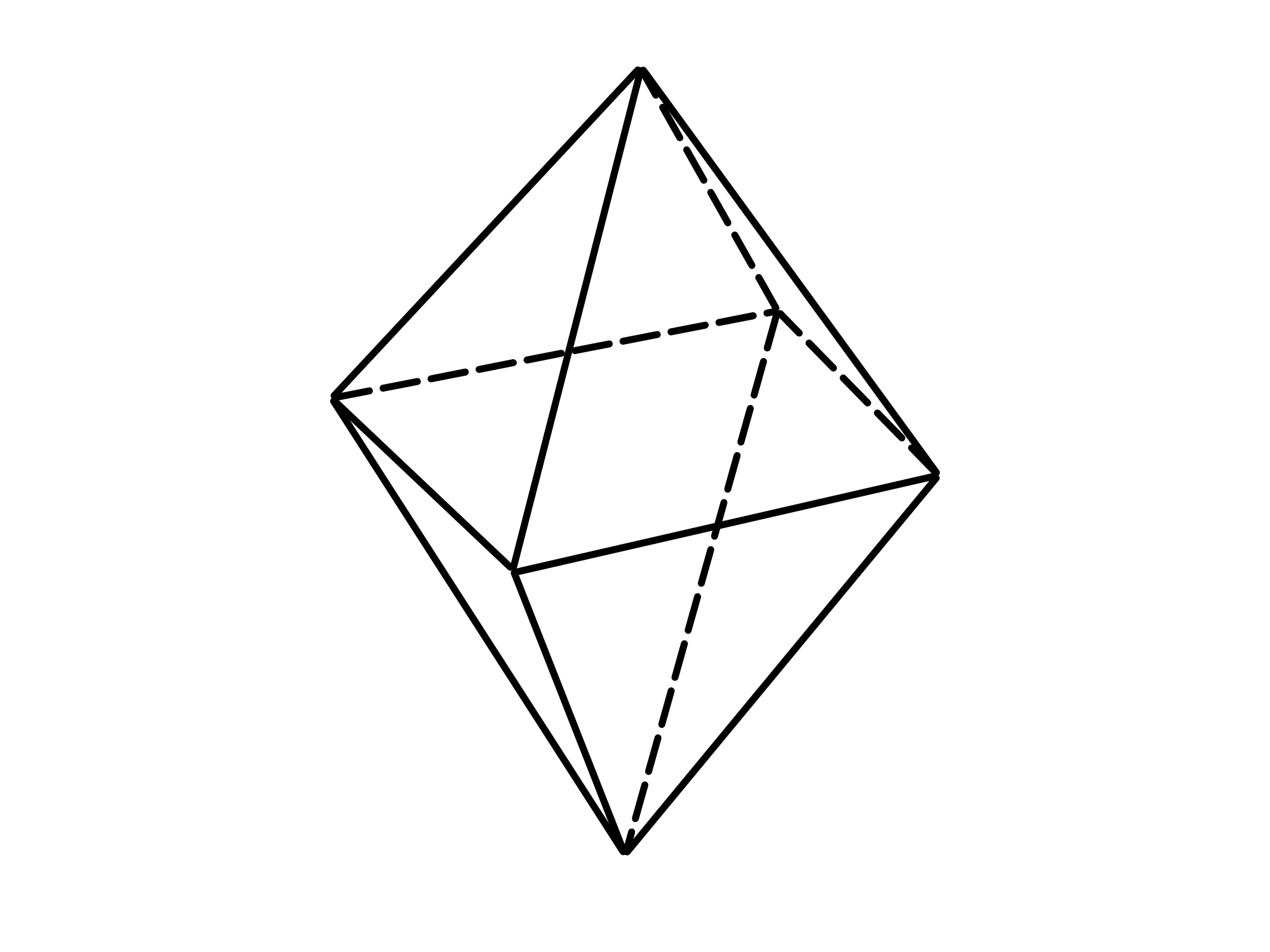
L'ottaedro regolare:
Il dodecaedro regolare:
Infine, l'icosaedro regolare:
Se parlate greco antico, sarà facile per voi ricordarvi il loro nome perché sono formati dal numero di facce che hanno in greco antico più un suffiso -edro più l'aggettivo "regolare". Altrimenti dovrete impararli a memoria.
Completiamo con qualche famiglia di poliedri comuni da incontrare:
Qualche altro poliedro
Iniziamo con i prismi. I prismi sono poliedri convessi formati da due poligoni paralleli e uguali, chiamati basi, e da parallelogrammi come facce laterali:
Nella famiglia dei prismi rientrano pure i parallelopipedi. L'unico prisma che è anche un poliedro regolare è il cubo.
Le piramidi invece sono formate da una base e un vertice che non appertiene ad essa e tutte le facce laterali sono triangoli:
L'unica piramide che è anche un poliedro regolare è il tetraedro regolare. Tutte le altre piramidi sono poliedri irregolari.
Infine vediamo il tronco di piramide. Essa è ottenuta tagliando la piramide con un piano parallelo alla base:
Le facce laterali sono tutti trapezi e tutti i tronchi di piramide sono poliedri irregolari.
Finiamo osservando due proprietà dei poliedri:
Qualche proprietà
La formula di Eulero collega tra loro il numero di facce F, il numero di vertici V e il numero di spigoli S. Essa afferma che:
F+V=S+2
Conoscendo il numero di vertici e di spigoli, possiamo trovare anche il numero di diagonali D:
D= {V(V-1)\over 2} - S