Funzione logaritmica
Di seguito analizzeremo la funzione logaritmica.
Funzione logaritmica
Una funzione logaritmica è una funzione del tipo:
y=\log_{a} (x)
con a>0 e a\neq 1
Sappiamo già che la condizione di esistenza di un logaritmo, oltre a quelle scritte sopra, è che il suo argomento sia maggiore di 0. Quindi il dominio sarà formato da tutti i numeri reali positivi, ovvero da \mathbb{R} ^+.
La funzione logaritmica y=\log_{a} (x) è la funzione inversa della funzione esponenziale y=a^x , di conseguenza il suo grafico sarà uguale al simmetrico della funzione esponenziale rispetto alla retta y=x:
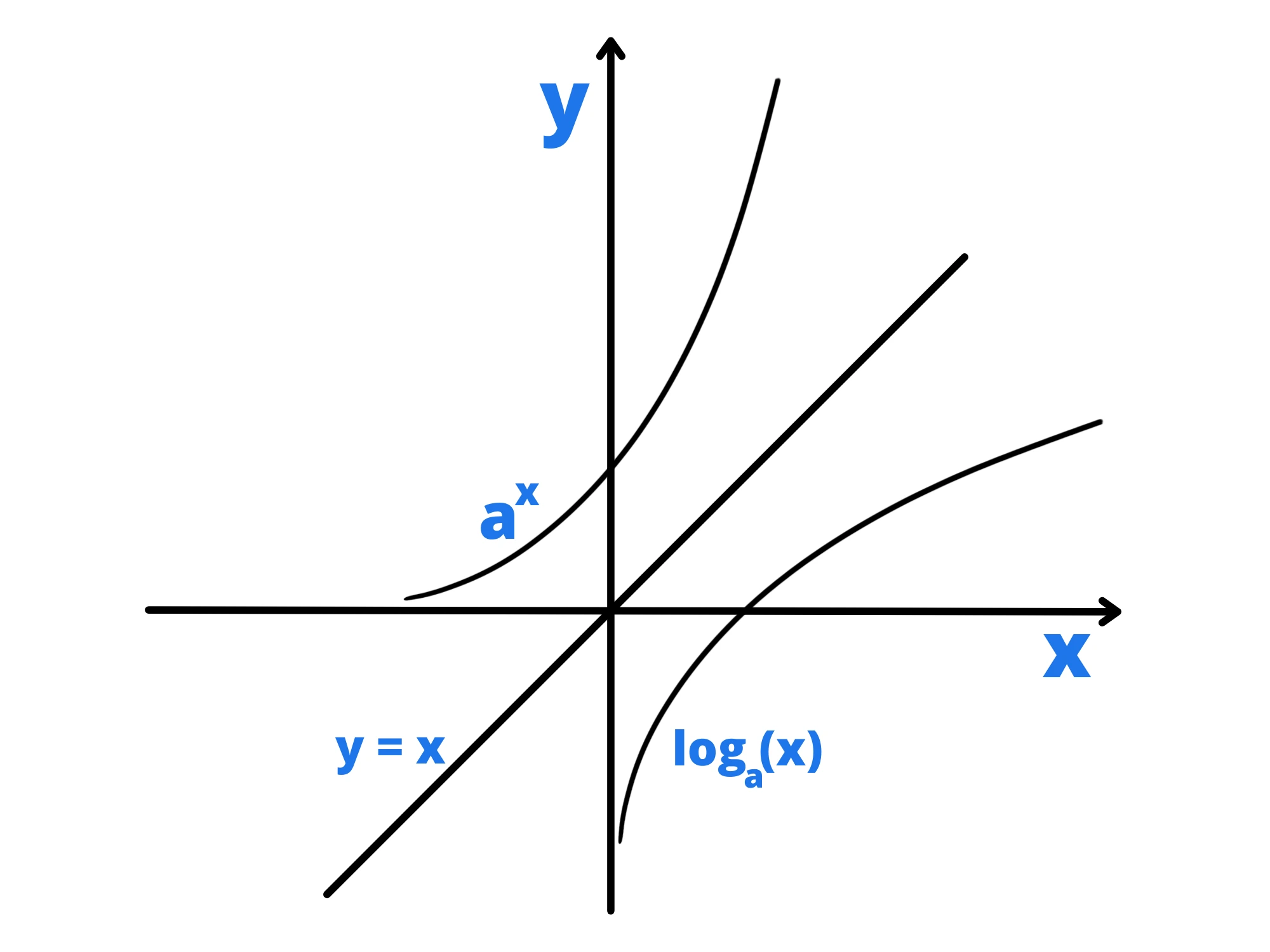
Per questo otteniamo che la funzione logaritmica deve essere monotona crescente (sempre crescente) per a>1, mentre sarà monotona decrescente (sempre decrescente) per 0< a < 1 .
Siccome per ogni a (che rispettano le condizioni di esistenza) abbiamo che:
\log_{a} (1) = 0
La funzione deve sempre passare per il punto (0;1).
Siccome, usando la formula del cambiamento di base, abbiamo:
\log_{1\over a} (x) = \frac{\log_{a}(x)}{\log_{a} ({1\over a})}={\log_{a} (x) \over -1 }=-\log_{a} (x)
y=\log_{1\over a} (x) è il simmetrico rispetto all'asse x della funzione y=\log_{a} (x).
Grafico di funzioni del tipo y=\ln(f(x))
Ricordiamo innanzitutto che \ln(x) è il logaritmo base e di x, dove e è il numero di Nepero. Normalmente si studia solo il caso di \ln(f(x)) perché non ci si vuole soffermare troppo su questo argomento e si studia solo il più comune.
Per le condizioni di esistenza (C.E.) del logaritmo, dobbiamo avere f(x)>0, altrimenti in quel punto \ln(f(x)) non esiste nei numeri reali.
Per tracciare un grafico con buona approssimazione vi basta poi ricordare che:
\ln(1) = 0
e che quando f(x) si avvicina a 0, \ln(x) diminuisce e quando f(x) aumenta, \ln(f(x) aumenta.