Funzioni esponenziali

Cos’è una funzione esponenziale?

Una funzione esponenziale è una funzione espressa da una potenza con base fissa ed esponente variabile, ovvero una funzione del tipo:

f(x)=a^x

Esempi di funzioni esponenziali sono:

f(x)=2^x

f(x)=4^x

f(x)={0.5}^{x}

g(x)={13.179}^x

Non sono invece funzioni esponenziali le seguenti:

f(x)=x^2 perché è espressa da una potenza con base variabile ed esponente fisso.

f(x)=2^3 perché è espressa da una potenza con base ed esponente fisso ed è in realtà una funzione costante.

Funzioni esponenziali con base maggiore di 1

Il grafico di una funzione esponenziale con base maggiore di 1 è fatto così:

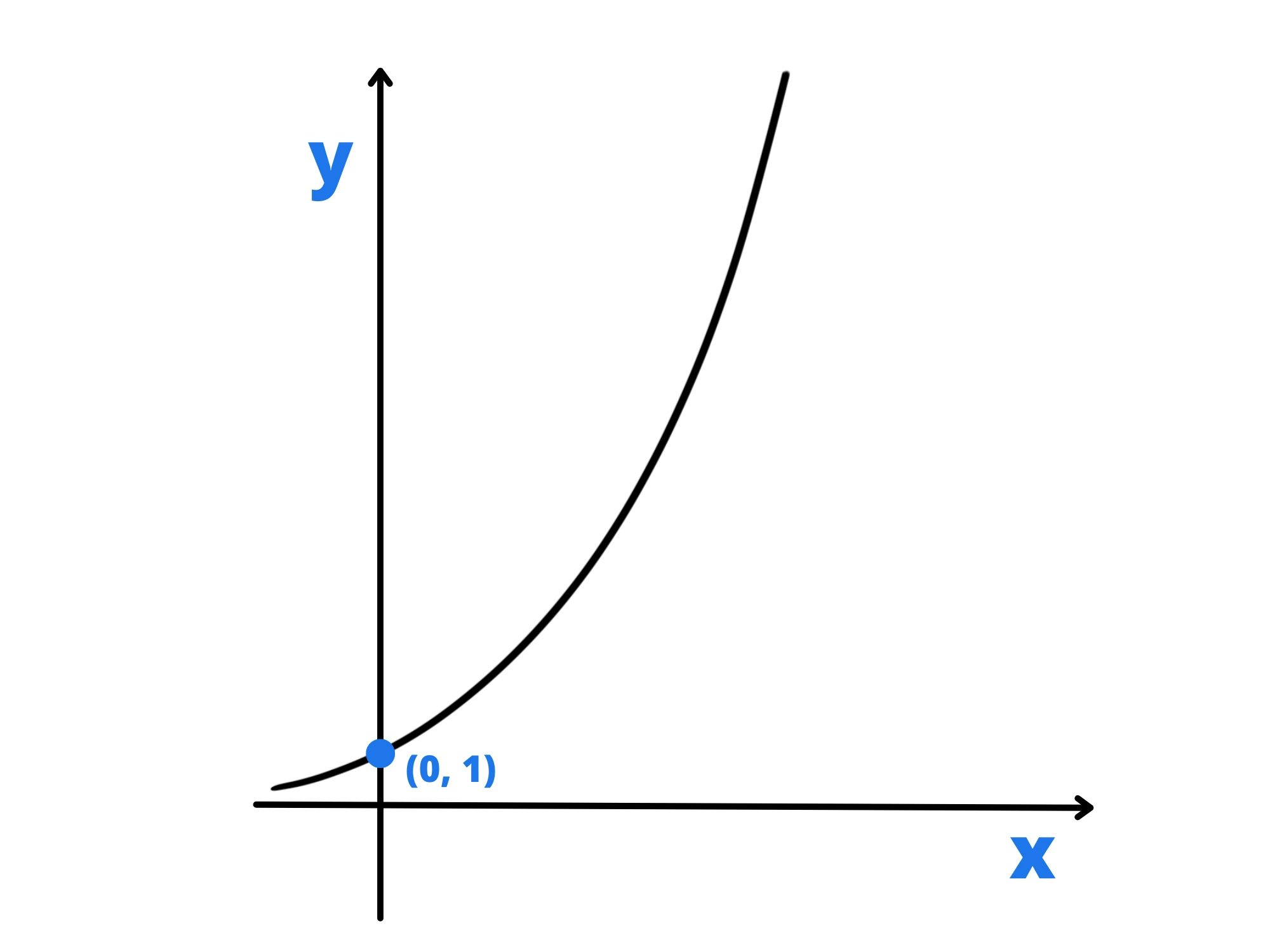
Osserviamo innanzitutto che si tratta di una funzione sempre positiva. Infatti la sua immagine I è l’intervallo (0;+\infty).

Poi notiamo che il grafico di qualsiasi funzione esponenziale interseca l'asse y sempre ad altezza 1 perché qualsiasi numero (diverso da 0) elevato alla 0 da sempre 1.

Inoltre è una funzione monotona crescente (aumenta sempre) ed è quindi anche biunivoca. Questo è molto importante perché ci permetterà di definire una funzione inversa, il logaritmo, che vedremo in un’altra lezione (qui).

Queste funzioni crescono molto velocemente, più di qualsiasi altra funzione polinomiale.

Pure se all'inizio aumentano lentamente, più si va avanti e più aumenta velocemente e prima o poi supererà qualsiasi funzione polinomiale. Questo andamento viene chiamato crescita esponenziale.

Per questo quando qualcosa cresce molto velocemente si dice che "sta aumentando esponenzialmente".

Funzione esponenziale con base compresa tra 0 ed 1

Nel caso in cui la base sia 1, siccome 1^n=1 per ogni n, otterremo la funzione continua f(x) = 1.

Stessa cosa nel caso in cui la base sia uguale a 0. L’unica differenza è che ad x=0 otterremo 0^0 che non è definito.

Per gli altri valori tra 0 ed 1, però, otteniamo delle funzioni più interessanti. Queste funzioni si comportano esattamente come quelle con base maggiore di 1, ma al contrario. Ovvero, sono anche loro sempre positive, ma questa volta sono monotone decrescenti e diminuiscono sempre più lentamente.

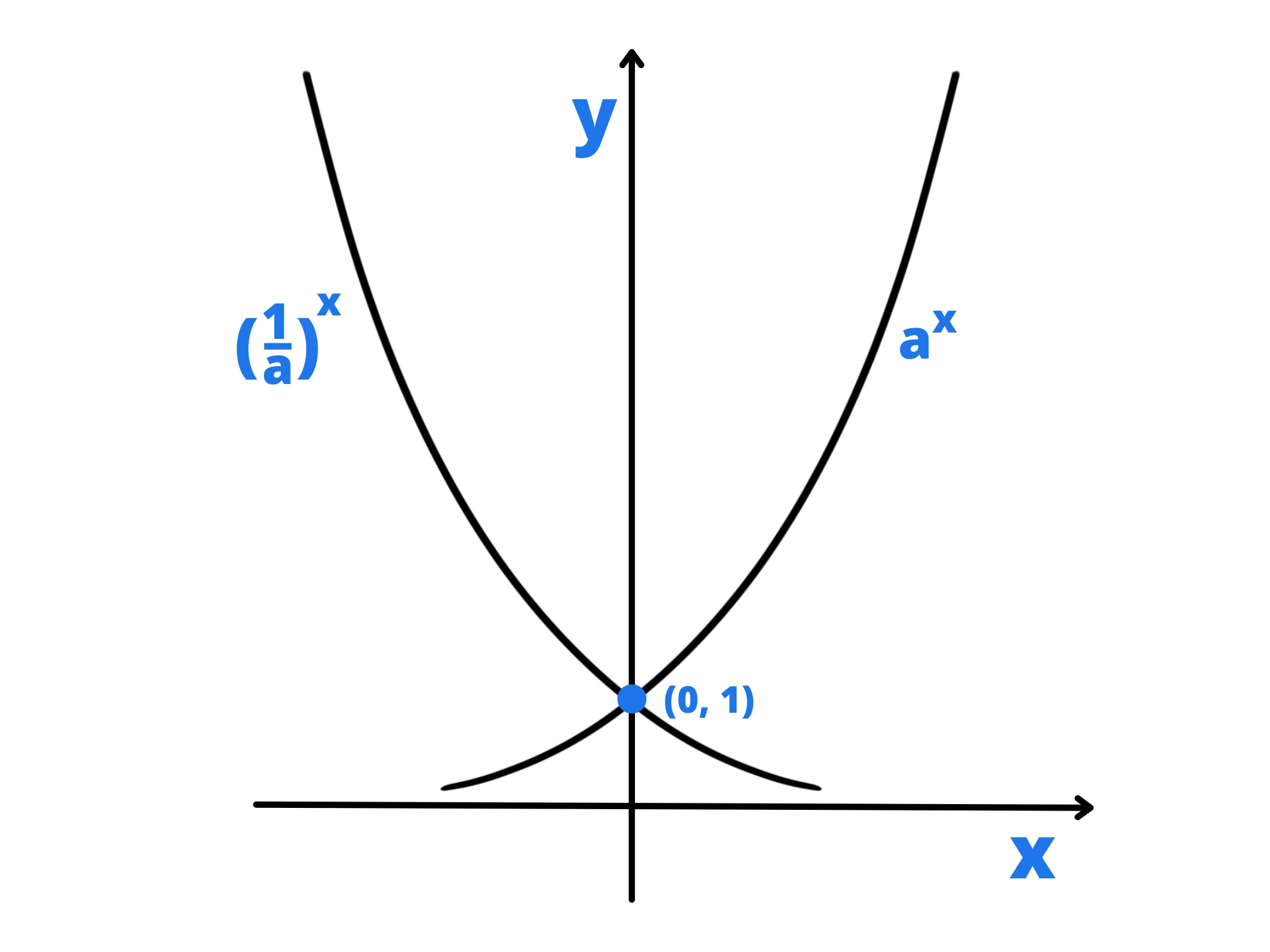
Perché avviene questo?

Prendiamo un numero b>1 con cui prendiamo la funzione esponenziale f(x)= b^x.

La funzione simmetrica rispetto all’asse y di f(x) è f(-x). Dunque il simmetrico g(x) dela nostra funzione sarà f(-x) = b^{-x}.

Grazie alle proprietà delle potenze possiamo riscriverla come g(x) = {1\over b^x}, cioè g(x) = {1\over b}^x.

1\over b è appunto un numero compreso tra 0 ed 1, perciò se tutte le funzioni esponenziali con base maggiori di 1 erano della stessa tipologia di f(x), tutte le funzioni esponenziali con base compresa tra 0 ed 1 saranno della tipologia di g(x). Per questo otteniamo quella simmetria.

Perché non possiamo prendere basi negative?

Questo perché funzioni esponenziali con basi negative hanno valori che non appartengono ai numeri reali. Ad esempio nel punto x={1\over 2}, la funzione vale:

f({1\over 2})=a^{1\over 2}=\sqrt{a}

Ed è impossibile nei numeri reali fare la radice quadrata di un numero negativo.

Oltre al caso x={1\over 2} abbiamo infiniti altri casi analoghi in cui non otteniamo valori reali, per questo non ci interessano per ora.

La funzione esponenziale e^x

Tra tutte le funzioni esponenziali ce n’è una che è più importante di tutte: quella che ha come base il Numero di Nepero.

Essa ha infatti alcune proprietà extra che la rendono veramente speciale, facendole ottenere un posto nell’Olimpo delle funzioni matematiche. Queste proprietà extra richiedono però matematica più avanzata e le studieremo più avanti.

Per adesso vi basta sapere che questo numero viene solitamente indicato con la lettera e e vale circa 2,71.

Talvolta infatti quando si dice “funzione esponenziale” è sottinteso che ci stiamo riferendo ad essa e non ad una funzione esponenziale generica. Spesso la troverete scritta come exp(x) (notazione usata dalla maggior parte delle calcolatrici scientifiche).