Disequazioni esponenziali

Cos'è una disequazione esponenziale?

Una disequazione esponenziale è una disequazione in cui appare almeno una potenza con l'incognita nell'esponente. Esse sono quindi disequazioni del tipo:

a^{f(x)} > g(x)

o con < ,\geq o \leq al posto di >.

Iniziamo vedendo il caso particolare in cui f(x) = x e g(x) è costante. Avremo quindi disequazioni del tipo:

a^x > b

Dobbiamo dividere queste disequazioni in due casi:

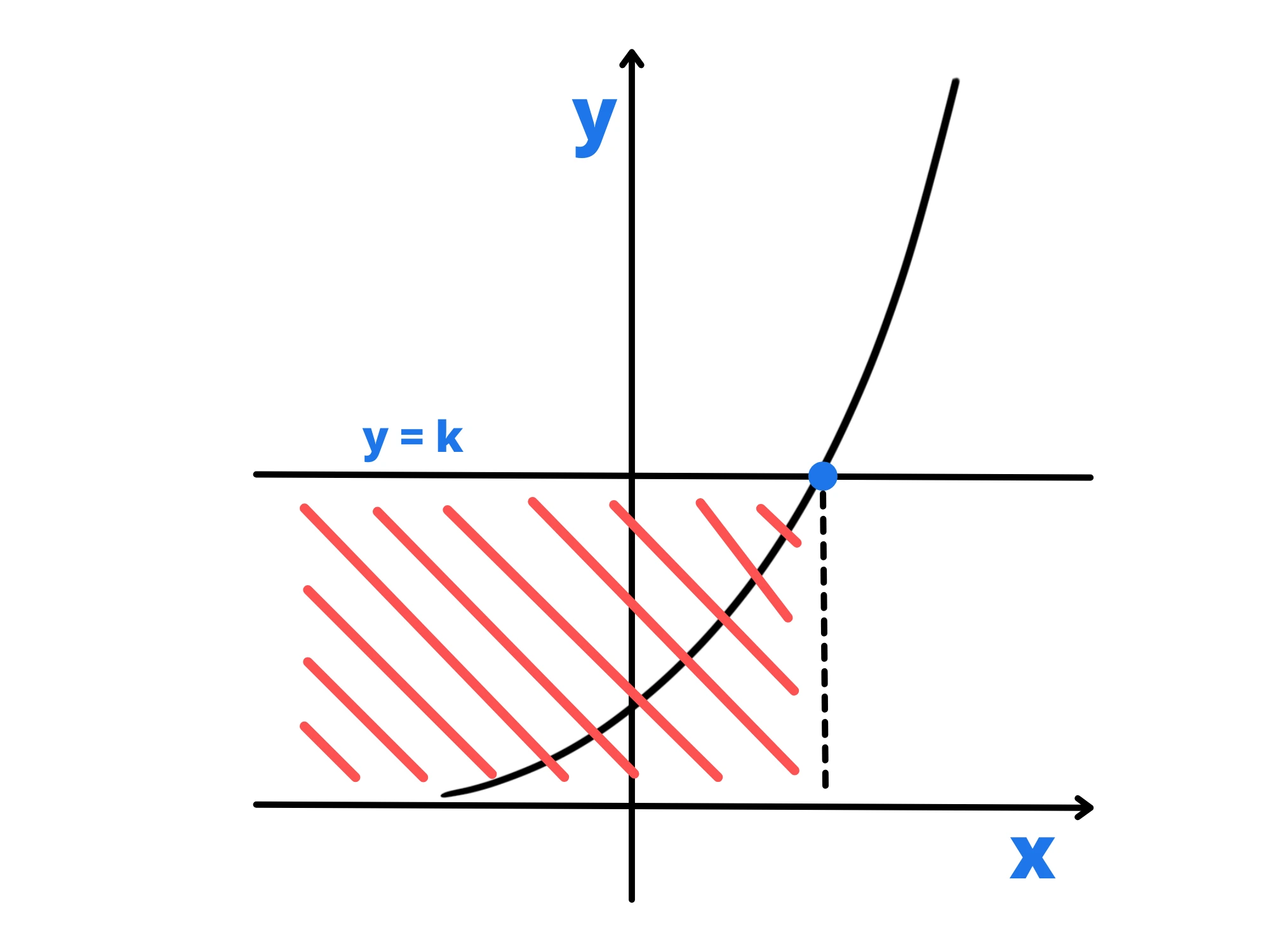
La base a è maggiore di 1

In questo caso per prima cosa risolviamo l'equazione associata:

a^x =b

Una volta fatto questo, sapendo che la funzione a^x è monotona crescente (ovvero aumenta sempre), troviamo la soluzione della disequazione.

Vediamo qualche esempio.

Risolviamo la disequazione esponenziale:

3^x > 81

Risolviamo l'equazione associata:

3^x = 81

3^x = 3^4

x= 4

Sappiamo che 3^x aumenta sempre, quindi per x > 4 sarà sempre maggiore di 81. Quindi la soluzione è x>4.

Risolviamo la disequazione esponenziale:

5^x \leq 125

Risolviamo l'equazione associata:

5^x = 125

5^x = 5^3

x= 3

Sappiamo che 5^x aumenta sempre, quindi per x>3 sarà sempre maggiore di 125, mentre per x < 3 sarà sempre minore di 125. La soluzione è quindi x \leq 3.

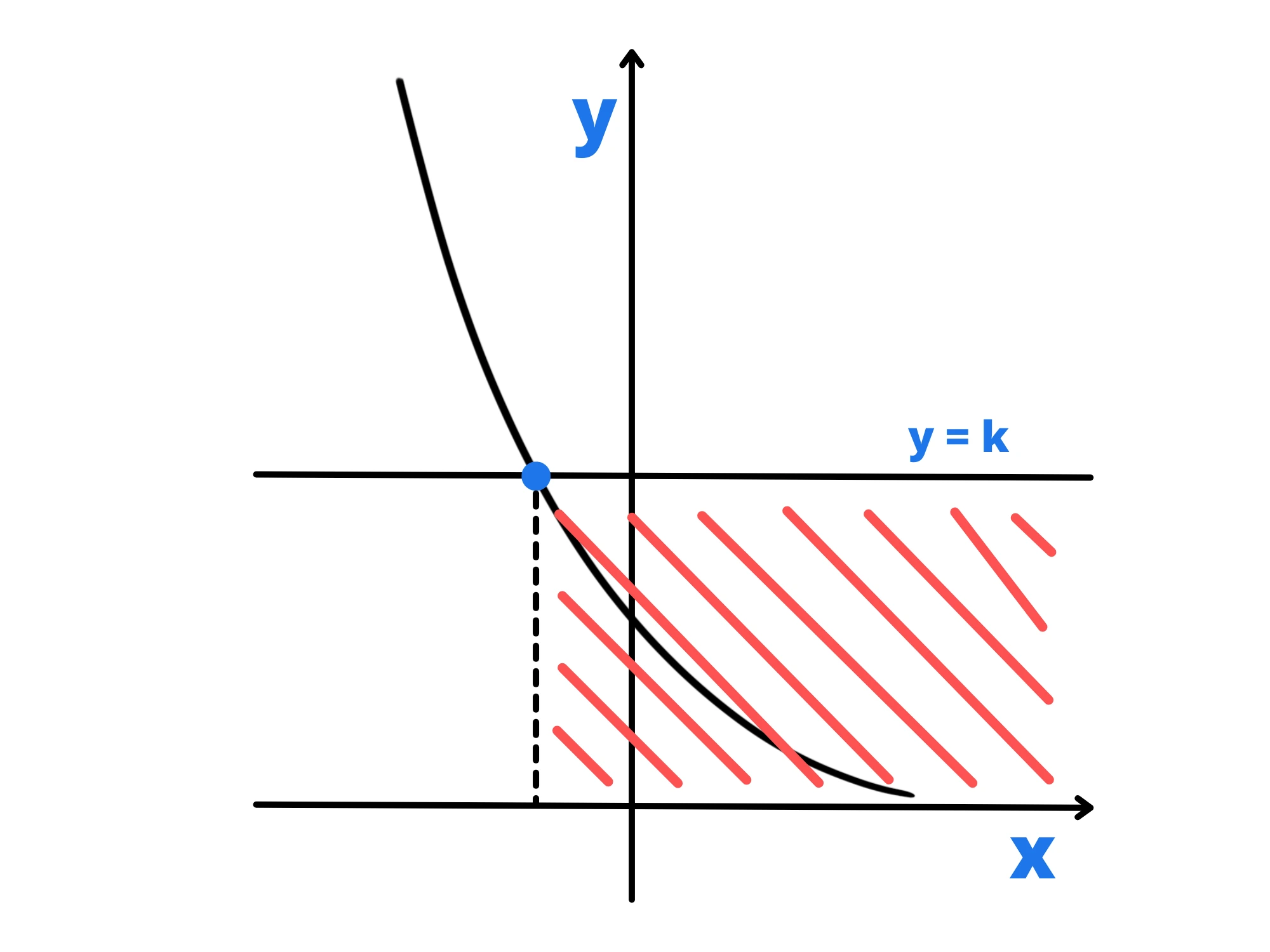
La base a è compresa tra 0 e 1

In tal caso il procedimento è lo stesso, ma questa volta la funzione sarà monotona decrescente (ovvero diminuisce sempre).

Vediamo qualche esempio:

Risolviamo la disequazione esponenziale:

({1 \over 2})^x < {1\over 32}

Risolviamo l'equazione associata:

({1\over 2})^x ={1\over 32}

({1\over 2})^x =({1\over 2})^5

x=5

Siccome ({1\over 2})^x diminuisce sempre, per x>5 sarà sempre minore di {1\over 32}, quindi la soluzione è proprio x>5.

Risolviamo la disequazione esponenziale:

({1\over 3})^x \geq {1\over 9}

Risolviamo l'equazione associata:

({1\over 3})^x ={1\over 9}

({1\over 3})^x =({1\over 3})^2

x=2

Siccome ({1\over 3})^x diminuisce sempre, per x>2 sarà sempre minore di {1\over 9} e sarà invece maggiore di {1\over 9} per x < 2, quindi la soluzione è proprio x\leq 2.

Disequazioni esponenziali risolvibili con i logaritmi

Usando i logaritmi possiamo risolvere disequazioni esponenziali più complicate, dove possono apparire più potenze con incognite all'esponente. Ci basterà applicare il logaritmo base 10 da entrambi i lati e semplificare. Possiamo pure applicare logaritmi con altre basi, ma se è compresa tra 0 ed 1 dobbiamo cambiare il segno della disequazione, perché:

Dato x>y, se a>1, avremo:

\log_{a} (x) >\log_{a} (y)

Mentre se 0 < a < 1 , avremo:

\log_{a} (x) < \log_{a} (y)

In generale conviene quindi applicare sempre il logaritmo base 10 e non avere paura di dover cambiare qualcosa.

Vediamo qualche esempio:

Risolviamo la disequazione esponenziale:

5\cdot 3^x > 2^{x-3}

Abbiamo quantità positive da entrambi i lati, quindi applichiamo il logaritmo base 10 da entrambi i lati:

\log_{10}(5 \cdot 3^x) > \log_{10}(2^{x-3})

Applichiamo la proprietà del logaritmo di un prodotto e sottintendiamo \log_{10} con \log:

\log (5) + \log (3^x) > \log (2^{x-3})

Applichiamo la proprietà del logaritmo di una potenza ed isoliamo x:

\log(5) + x \log(3) > (x-3) \log(2)

\log (5) + x\log (3) >x\log(2) -3\log(2)

x\log(3) - x\log(2) > -\log(5) -3\log(2)

x( \log(3) -\log(2))>-(\log(5)+3\log(2))

Siccome \log(3) -\log(2) è una quantità positiva, possiamo dividere entrambi i lati per essa:

x> -\frac{\log(5)+3\log(2)}{\log(3)-\log(2)}