Disequazioni di 2°grado
Di seguito analizzeremo le disequazioni di 2°grado.
Disequazioni di secondo grado
Le disequazioni di secondo grado sono equazioni di secondo grado con la differenza che al posto di porre una condizione di uguaglianza tra i membri se ne pone una di disuguaglianza che può essere maggiore o minore, ma anche maggiore o uguale o minore o uguale
Di seguito alcuni esempi di disequazioni di secondo grado:
• 3x^2-x+ \sqrt3 \geq 0
• x^2+6x-16<0
• \sqrt2x^2-2x+3 \leq 0
Risoluzione delle equazioni di secondo grado
Per risolvere una disequazione di secondo grado basterà studiare il variare del segno della disequazione in funzione di x e prendere quei valori per i quali è soddisfatta la condizione di disuguaglianza.
Vediamo un esempio:
3x-x+5 \leq 2x^2+1
Portiamo tutti i termini da un lato in modo da ottenere 0 dall’altro:
-x^2+x+2 \leq 0
Ora risolviamo l'equazione associata (-x^2 +x +2 =0 ) usando la formula risolutrice delle equazioni di secondo grado:
-x^2+x+2 =0 \longrightarrow x_{1;2}={-1 \pm \sqrt{1+4 \cdot2} \over -2} \longrightarrow x_1=-1; x_2 =2
Avendo calcolato le soluzioni, sappiamo per quali x il polinomio -x^2 +2x +2 sarà 0. Come si può sapere quando invece sarà positiva o negativa?
Studio della parabola
Per rispondere a questa domanda possiamo fare un passo indietro e ragionare sul polinomio di secondo grado in se: come visto nelle lezioni precedenti, il grafico di un polinomio di secondo grado sul piano cartesiano è una parabola.

Posizione rispetto alle ascisse
E quindi? Osservando con uno sguardo attento ci si può accorgere che la parabola può solo essere posizionata in 3 modi rispetto all’asse delle ascisse (x):
1. Intersecarla in 2 punti distinti (il nostro caso)

2. Intersecarla in 2 punti coincidenti

3. Non intersecarla affatto (2 soluzioni complesse e coniugate)
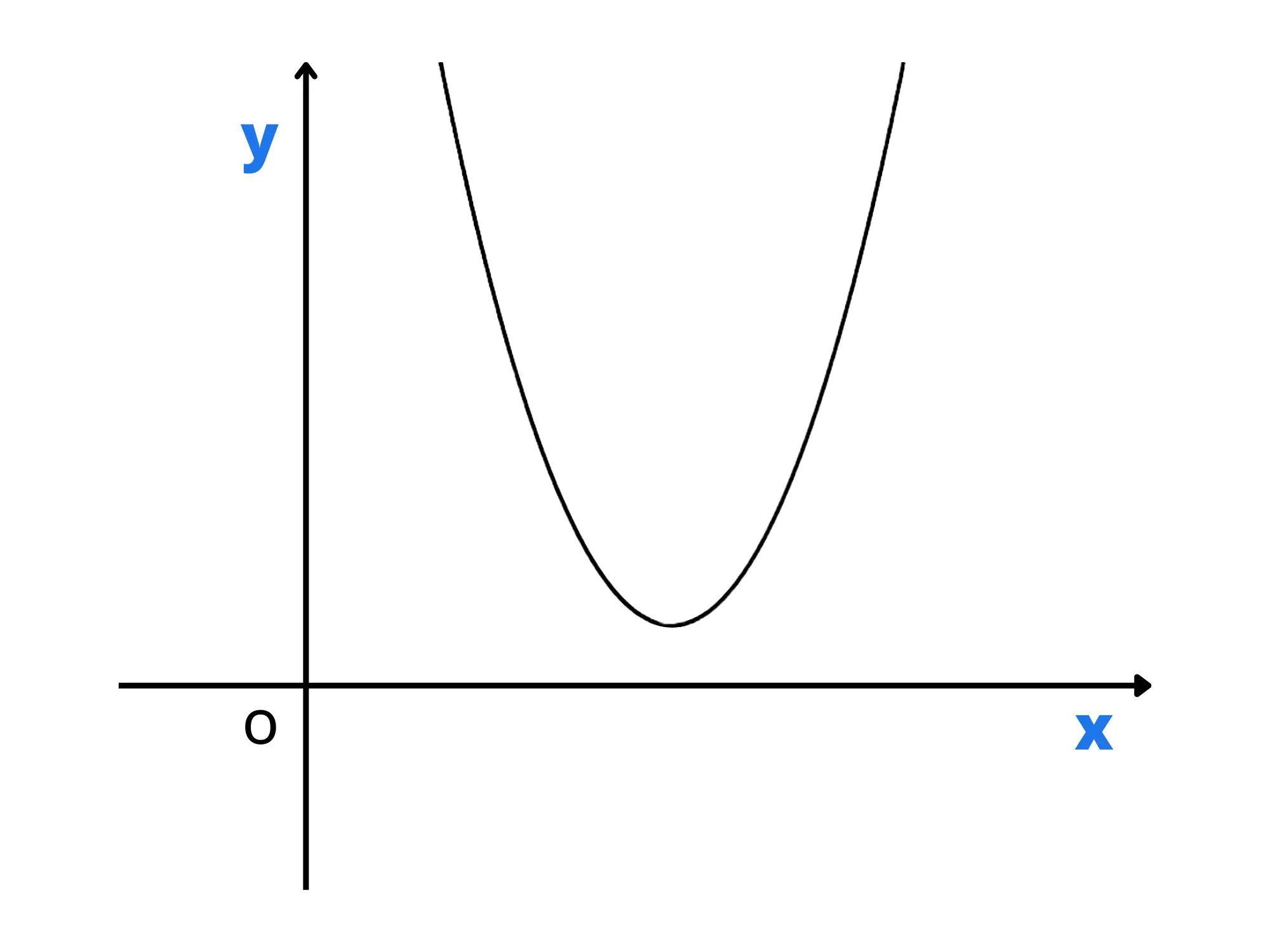
Questa informazione la ricaviamo dalle 2 soluzioni trovate in precedenza.
x_1=-1; x_2 =2
Orientamento
Per l’orientamento della parabola invece, basterà guardare il coefficiente del primo termine dell’equazione (il coefficiente di x^2). Se questo è positivo avrà una concavità verso l’alto, se negativo invece verso il basso.
\rightarrow -x^2\leftarrow +x+2 \leq 0

Questo si può ricordare facilmente pensando a una faccia, se positiva la bocca sarà una parabola verso l’alto, se negativa questa sarà verso il basso.

Ora che sappiamo tutto su questa parabola possiamo arrivare al risultato finale:
Trovare le soluzioni
Quando la parabola si trova sopra l'asse x, vuol dire che il nostro polinomio è maggiore di 0, mentre quando si trova sotto l'asse x il nostro polinomio è negativo.
Quindi se vogliamo sapere quando il polinomio sarà negativo, ci basterà guardare quando la parabola è sotto l'asse delle x.
La parabola in questo caso è concava verso il basso perché il coefficiente del primo termine è negativo.

Quindi, guardando il grafico, il risultato della disequazione sono tutte le x minori o uguali alla soluzione più piccola dell’equazione associata e tutte le x maggiori o uguale alla soluzione più grande.
x_1=-1; x_2 =2

Soluzione: x\leq-1 \vee x\geq 2
Metodo alternativo
Un altro modo per risolvere le disequazioni di secondo grado è di fattorizzare il nostro polinomio e controllare il segno di ogni fattore singolarmente e poi quello del loro prodotto.
Esempio:
x^2+x-2 \geq0
Fattorizzazione:
(x+2)\cdot (x-1) \geq 0
Un modo semplice per fattorizzare un polinomio è cercare i due numeri la cui somma sia il coefficiente di x e il cui prodotto sia il termine noto.
Una volta fattorizzato il polinomio otterremo qualcosa del genere (x+g) \cdot (x+r).
Prima ci chiederemo quando x+g è positivo e quando negativo. Poi passeremo a x+r ed infine tracceremo il grafico dei segni.
Nel nostro caso abbiamo:
x+2 > 0 \longrightarrow x > -2
x-1>0 \longrightarrow x>1
Quindi il grafico dei segni sarà il seguente:
Dunque negli intervalli in cui il loro segno sarà uguale, il prodotto sarà positivo, mentre dove saranno di segni discordi il prodotto sarà negativo.
La soluzione della nostra disequazione sarà dunque x \leq -2 \vee x \geq 1.
Forniamo un altro esempio per chiarire meglio:
Dato il polinomio x^2+3x-4 trovare per quali valori di x esso risulta essere maggiore di 0.
Notiamo che esso è fattorizzabile in (x+4) \cdot (x-1). Dunque analizziamo i singoli termini.
x+4 è uguale a 0 quando x=-4, è maggiore di 0 quando x > -4 e minore di 0 quando x<-4.
x-1 è uguale a 0 quando x=1, è maggiore di 0 quando x>1 e minore di 0 quando x< 1.
Soprattutto in casi più complicati tracciamo il seguente grafico, dove indichiamo con una retta continua i valori positivi, con una retta tratteggiata i valori negativi e con delle rette verticali gli 0:

Dunque le soluzioni saranno x < -4 \vee x > 1.
1.
Risolvere la disequazione 2x^2 - 3x - 5 > 0 .
x < -1 o x > \frac{5}{2}
1. Risolviamo l'equazione associata 2x^2 - 3x - 5 = 0 . Le radici sono x = -1 e x = \frac{5}{2} .
2. Determiniamo i segni della disequazione. Poiché il coefficiente di x^2 è positivo, la parabola si apre verso l'alto. Quindi, la disequazione è soddisfatta per i valori al di fuori dell'intervallo tra le radici.
x < -1 o x > \frac{5}{2}
2.
Risolvere la disequazione x^2 - 4x + 3 < 0 .
1 < x < 3
1. Risolviamo l'equazione associata x^2 - 4x + 3 = 0 . Le radici sono x = 1 e x = 3 .
2. Determiniamo i segni della disequazione. La parabola si apre verso l'alto, quindi la disequazione è soddisfatta tra le radici.
1 < x < 3
3.
Risolvere la disequazione 5x^2 - 7x + 2 \geq 0 .
x \leq \frac{2}{5} o x \geq 1 .
1. Risolviamo l'equazione associata 5x^2 - 7x + 2 = 0 . Le radici sono x = \frac{2}{5} e x = 1 .
2. Determiniamo i segni della disequazione. La parabola si apre verso l'alto, quindi la disequazione è soddisfatta al di fuori dell'intervallo tra le radici.
x \leq \frac{2}{5} o x \geq 1 .
4.
Risolvere la disequazione x^2 + 5x - 6 \leq 0 .
-6 \leq x \leq 1 .
1. Risolviamo l'equazione associata x^2 + 5x - 6 = 0 . Le radici sono x = -6 e x = 1 .
2. Determiniamo i segni della disequazione. La parabola si apre verso l'alto, quindi la disequazione è soddisfatta tra le radici.
-6 \leq x \leq 1 .
5.
Risolvere la disequazione 4x^2 - 12x + 9 > 0 .
x \neq \frac{3}{2} .
1. Risolviamo l'equazione associata 4x^2 - 12x + 9 = 0 . La radice è x = \frac{3}{2} .
2. Determiniamo i segni della disequazione. La parabola si apre verso l'alto e ha una radice doppia, quindi la disequazione è soddisfatta per tutti i valori di x tranne x = \frac{3}{2} .
x \neq \frac{3}{2} .
6.
Risolvere la disequazione 3x^2 + 4x - 7 < 0 .
-\frac{7}{3} < x < 1 .
1. Risolviamo l'equazione associata 3x^2 + 4x - 7 = 0 . Le radici sono x = -\frac{7}{3} e x = 1 .
2. Determiniamo i segni della disequazione. La parabola si apre verso l'alto, quindi la disequazione è soddisfatta tra le radici.
-\frac{7}{3} < x < 1 .
7.
Risolvere la disequazione x^2 - x - 2 \geq 0 .
x \leq -1 o x \geq 2 .
1. Risolviamo l'equazione associata x^2 - x - 2 = 0 . Le radici sono x = -1 e x = 2 .
2. Determiniamo i segni della disequazione. La parabola si apre verso l'alto, quindi la disequazione è soddisfatta al di fuori dell'intervallo tra le radici.
x \leq -1 o x \geq 2 .
8.
Risolvere la disequazione 2x^2 - 5x + 3 \leq 0 .
1 \leq x \leq \frac{3}{2}
1. Risolviamo l'equazione associata 2x^2 - 5x + 3 = 0 . Le radici sono x = 1 e x = \frac{3}{2} .
2. Determiniamo i segni della disequazione. La parabola si apre verso l'alto, quindi la disequazione è soddisfatta tra le radici.
1 \leq x \leq \frac{3}{2}
9.
Risolvere la disequazione x^2 - 6x + 8 > 0 .
x < 2 o x > 4 .
1. Risolviamo l'equazione associata x^2 - 6x + 8 = 0 . Le radici sono x = 2 e x = 4 .
2. Determiniamo i segni della disequazione. La parabola si apre verso l'alto, quindi la disequazione è soddisfatta al di fuori dell'intervallo tra le radici.
x < 2 o x > 4 .
10.
Risolvere la disequazione 7x^2 - 14x + 7 \geq 0 .
x \in \mathbb{R}
1. Risolviamo l'equazione associata 7x^2 - 14x + 7 = 0 . La radice è x = 1 .
2. Determiniamo i segni della disequazione. Poiché abbiamo una radice doppia e la parabola si apre verso l'alto, la disequazione è soddisfatta per tutti i valori di x .
x \in \mathbb{R}